Izotop fluoru
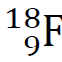
ulega rozpadowi promieniotwórczemu w wyniku przemiany β
+. Podczas rozpadu jądra tego izotopu fluoru powstają: cząstka β
+, jądro pewnego pierwiastka, który oznaczymy jako X, oraz tzw. neutrino elektronowe ν. Neutrino ma zerowy ładunek elektryczny, a jego masę możemy pominąć.
Masy jąder i cząstek uczestniczących w opisanym rozpadzie β+, wyrażone w jednostkach atomowych, mają następujące wartości:
𝑚
F = 17,99600 u – masa jądra fluoru
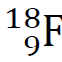
𝑚X = 17,99477 u – masa powstałego jądra
𝑚β = 0,00055 u – masa cząstki β+
𝑚ν = 0,00000 u – masę neutrina pomijamy.
Informacja do zadania 11.1.
Próbka z izotopem
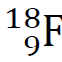
jest badana przez licznik promieniowania, który pokazuje całkowitą liczbę rozpadów β
+ jąder tego izotopu fluoru po upływie danego czasu (od rozpoczęcia pomiaru). Liczbę jąder izotopu fluoru
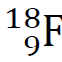
, znajdujących się w próbce w chwili początkowej, oznaczymy jako 𝑁
0. Łączną liczbę jąder, które uległy temu rozpadowi po upływie czasu 𝑡 od chwili początkowej 𝑡
0 = 0 min, oznaczymy jako 𝑁
𝑟.
Na wykresie poniżej przedstawiono zależność ilorazu 𝑁𝑟 ⁄𝑁0 od czasu 𝑡.
![]()




