Sonda kosmiczna o masie
m = 104 kg początkowo poruszała się swobodnie (jedynie pod wpływem grawitacji) dookoła Ziemi po orbicie kołowej o promieniu
r, z prędkością orbitalną o wartości
vor = 7,56 km/s (zobacz rys. 1.). W pewnym momencie włączono silniki odrzutowe sondy, odpowiednio zaprogramowane. Przez pewien czas na sondę działała siła odrzutu tak, że sonda poruszała się nadal po orbicie kołowej o promieniu
r, a wartość prędkości tej sondy rosła (zobacz rys. 2.). Gdy sonda osiągnęła prędkość
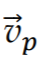
w chwili
tp, silniki odrzutowe wyłączono (zobacz rys. 3.), a sonda zaczęła się oddalać od Ziemi.
Prędkość
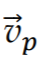
uzyskana przez sondę w odległości
r od środka Ziemi była na tyle duża, że umożliwiała sondzie
ciągłe oddalanie się od Ziemi oraz osiągnięcie w bardzo dalekiej odległości (gdzie wpływ pola grawitacyjnego Ziemi jest pomijalny) stałej prędkości o wartości
v∞ = 2,00 km/s (zobacz rys. 4.). Masa Ziemi wynosi
M = 5,97 ⋅ 1024 kg.
Do analizy zagadnienia przyjmij uproszczony model zjawiska, w którym:
• pomijamy oddziaływanie sondy ze Słońcem oraz innymi ciałami, a także ruch orbitalny Ziemi
• pomijamy zmianę masy sondy podczas działania silników odrzutowych
• zakładamy, że energia potencjalna sondy bardzo daleko od Ziemi – gdzie wpływ grawitacji ziemskiej jest pomijalny – wynosi zero (zobacz rys. 4.): Epot ∞ = 0.
![]()




