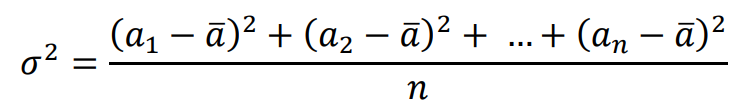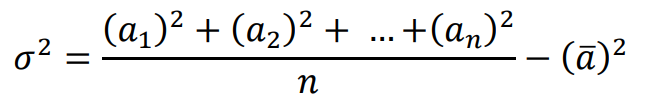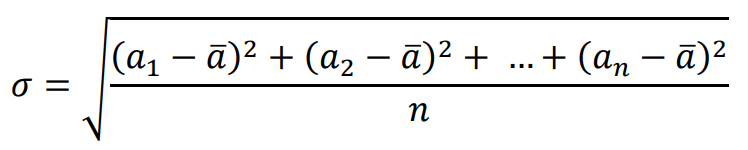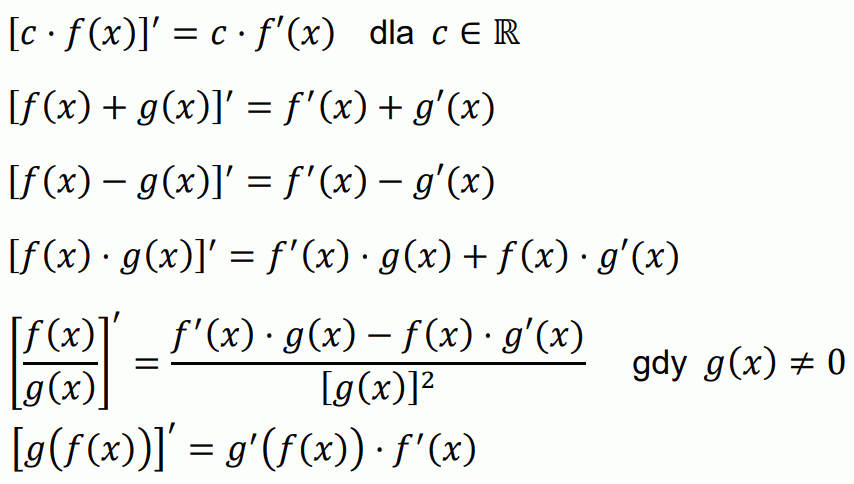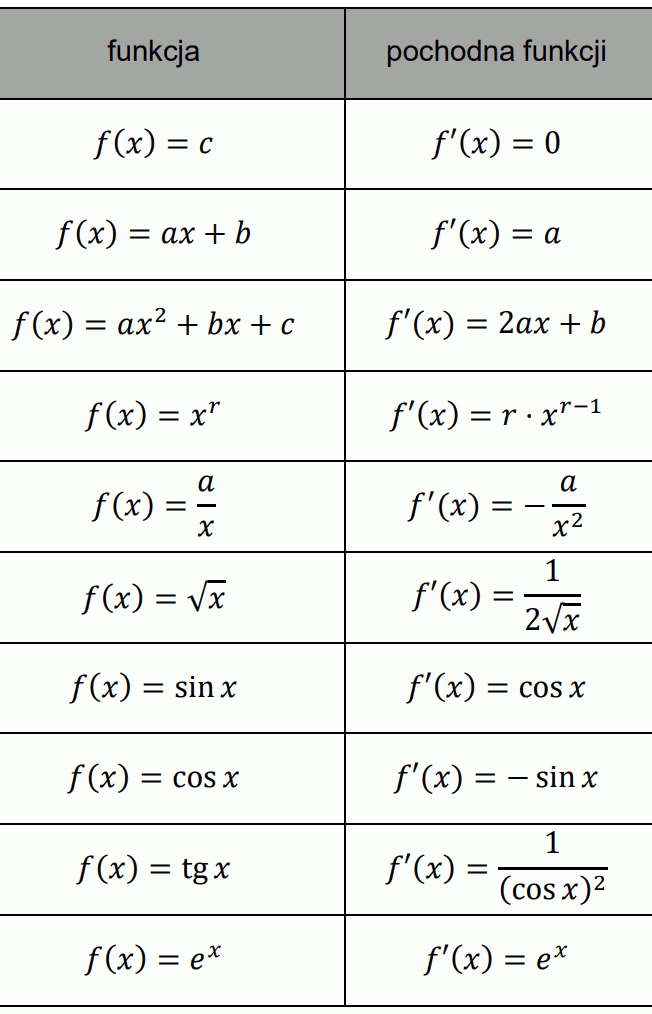Spis treści
⇑1. WARTOŚĆ BEZWZGLĘDNA LICZBY
• Wartość bezwzględną liczby rzeczywistej 𝑥 definiujemy wzorem:
• Dla dowolnej liczby 𝑥 mamy:
|𝑥| ≥ 0
|𝑥| = 0 wtedy i tylko wtedy, gdy 𝑥 = 0
|− 𝑥| = |𝑥|
Dla dowolnych liczb rzeczywistych 𝑥, 𝑦 mamy:
|𝑥 + 𝑦| ≤ |𝑥| + |𝑦|
|𝑥 − 𝑦| ≤ |𝑥| + |𝑦|
|𝑥 ⋅ 𝑦| = |𝑥| ⋅ |𝑦|
Ponadto, jeśli 𝑦 ≠ 0, to:
• Dla dowolnych liczb rzeczywistych 𝑎 oraz 𝑟 ≥ 0 mamy:
|𝑥 − 𝑎| ≤ 𝑟 wtedy i tylko wtedy, gdy 𝑎 − 𝑟 ≤ 𝑥 ≤ 𝑎 + 𝑟
|𝑥 − 𝑎| ≥ 𝑟 wtedy i tylko wtedy, gdy 𝑥 ≤ 𝑎 − 𝑟 lub 𝑥 ≥ 𝑎 + 𝑟
• Niech 𝑛 będzie liczbą całkowitą dodatnią. Dla dowolnej liczby rzeczywistej 𝑎 definiujemy jej 𝑛-tą potęgę:
• Pierwiastkiem arytmetycznym 𝑛√𝑎 stopnia 𝑛 z liczby 𝑎 ≥ 0 nazywamy liczbę 𝑏 ≥ 0 taką, że 𝑏𝑛 = 𝑎.
W szczególności, dla każdej liczby rzeczywistej 𝑎 prawdziwa jest równość:
Jeżeli 𝑎 < 0 oraz liczba 𝑛 jest nieparzysta, to 𝑛√𝑎 oznacza liczbę 𝑏 < 0 taką, że 𝑏𝑛 = 𝑎.
W zbiorze liczb rzeczywistych pierwiastki stopni parzystych z liczb ujemnych nie istnieją.
• Niech 𝑚, 𝑛 będą liczbami całkowitymi dodatnimi. Definiujemy:
• Niech 𝑟, 𝑠 będą dowolnymi liczbami rzeczywistymi. Jeśli 𝑎 > 0 i 𝑏 > 0, to:
Jeżeli wykładniki 𝑟, 𝑠 są liczbami całkowitymi, to powyższe wzory obowiązują dla wszystkich liczb 𝑎 ≠ 0 i 𝑏 ≠ 0.
• Niech 𝑥, 𝑦 będą dowolnymi liczbami rzeczywistymi.
Jeżeli 𝑎 ∈ (0, 1), to nierówność 𝑎𝑥 < 𝑎𝑦 jest równoważna nierówności 𝑥 > 𝑦.
Jeżeli 𝑎 ∈ (1, +∞), to nierówność 𝑎𝑥 < 𝑎𝑦 jest równoważna nierówności 𝑥 < 𝑦.
⇑3. LOGARYTMY
• Niech 𝑎 > 0 i 𝑎 ≠ 1. Logarytmem log𝑎 𝑏 liczby 𝑏 > 0 przy podstawie 𝑎 nazywamy wykładnik 𝑐 potęgi, do której należy podnieść 𝑎, aby otrzymać 𝑏:
log𝑎 𝑏 = 𝑐 wtedy i tylko wtedy, gdy 𝑎𝑐 = 𝑏
Równoważnie:
• Dla dowolnych liczb rzeczywistych 𝑥 > 0, 𝑦 > 0 oraz 𝑟 prawdziwe są równości:
Wzór na zamianę podstawy logarytmu:
jeżeli 𝑎 > 0, 𝑎 ≠ 1, 𝑏 > 0, 𝑏 ≠ 1 oraz 𝑐 > 0, to
W szczególności:
Zapisy log 𝑥 oraz lg 𝑥 oznaczają log10 𝑥.
⇑4. SILNIA. WSPÓŁCZYNNIK DWUMIANOWY
• Silnią liczby całkowitej dodatniej 𝑛 nazywamy iloczyn kolejnych liczb całkowitych od 1 do 𝑛 włącznie:
𝑛! = 1 ⋅ 2 ⋅ … ⋅ 𝑛
Ponadto przyjmujemy umowę, że 0! = 1.
Dla dowolnej liczby całkowitej 𝑛 ≥ 0 prawdziwa jest równość:
(𝑛 + 1)! = 𝑛! ⋅ (𝑛 + 1)
• Dla liczb całkowitych 𝑛, 𝑘 spełniających warunki 0 ≤ 𝑘 ≤ 𝑛 definiujemy współczynnik dwumianowy
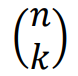
(symbol Newtona):
Prawdziwe są równości:
⇑5. WZÓR DWUMIANOWY NEWTONA
Dla dowolnej liczby całkowitej dodatniej 𝑛 oraz dla dowolnych liczb rzeczywistych 𝑎, 𝑏 mamy:
Dla dowolnej liczby całkowitej dodatniej 𝑛 oraz dla dowolnych liczb rzeczywistych 𝑎, 𝑏:
⇑6. WZORY SKRÓCONEGO MNOŻENIA
Dla dowolnych liczb rzeczywistych 𝑎, 𝑏:
Dla dowolnej liczby całkowitej dodatniej 𝑛 oraz dowolnych liczb rzeczywistych 𝑎, 𝑏 mamy:
W szczególności:
⇑7. FUNKCJA KWADRATOWA
• Wyróżnikiem Δ trójmianu kwadratowego 𝑎𝑥2 + 𝑏𝑥 + 𝑐 (𝑎 ≠ 0, 𝑏, 𝑐 ∈ ℝ) zmiennej rzeczywistej 𝑥 nazywamy liczbę
Δ = 𝑏² − 4𝑎𝑐
• Postać ogólna funkcji kwadratowej:
𝑓(𝑥) = 𝑎𝑥² + 𝑏𝑥 + 𝑐, 𝑎 ≠ 0, 𝑏, 𝑐 ∈ ℝ, 𝑥 ∈ ℝ .
• Wykresem funkcji kwadratowej jest parabola o wierzchołku w punkcie
Gdy 𝑎 < 0, to ramiona paraboli skierowane są ku dołowi. Gdy 𝑎 > 0, to ramiona paraboli skierowane są ku górze.
• Liczba miejsc zerowych funkcji kwadratowej 𝑓(𝑥) = 𝑎𝑥² + 𝑏𝑥 + 𝑐
(liczba pierwiastków trójmianu kwadratowego, liczba rzeczywistych rozwiązań równania kwadratowego 𝑎𝑥² + 𝑏𝑥 + 𝑐 = 0) zależy od wyróżnika Δ:
1. jeżeli 𝚫 > 𝟎, to funkcja kwadratowa ma dwa miejsca zerowe (trójmian kwadratowy ma dwa różne pierwiastki rzeczywiste, równanie kwadratowe ma dwa rozwiązania rzeczywiste):
2. jeżeli 𝚫 = 𝟎, to funkcja kwadratowa ma dokładnie jedno miejsce zerowe (trójmian kwadratowy ma jeden pierwiastek, równanie kwadratowe ma dokładnie jedno rozwiązanie rzeczywiste):
3. jeżeli 𝚫 < 𝟎, to funkcja kwadratowa nie ma miejsc zerowych (trójmian kwadratowy nie ma pierwiastków rzeczywistych, równanie kwadratowe nie ma rozwiązań rzeczywistych).
• Postać kanoniczna funkcji kwadratowej:
𝑓(𝑥) = 𝑎(𝑥 − 𝑝)² + 𝑞
• Jeżeli Δ ≥ 0, to funkcję kwadratową można przestawić w postaci iloczynowej
𝑓(𝑥) = 𝑎(𝑥 − 𝑥1)(𝑥 − 𝑥2)
• Wzory Viète’a
Jeżeli Δ ≥ 0, to
⇑8. CIĄGI
• Wzór na 𝑛-ty wyraz ciągu arytmetycznego (𝑎𝑛), określonego dla 𝑛 ≥ 1, o pierwszym wyrazie 𝑎1 i różnicy 𝑟:
𝑎𝑛 = 𝑎1 + (𝑛 − 1)𝑟
• Wzory na sumę 𝑆𝑛 początkowych 𝑛 wyrazów ciągu arytmetycznego:
• Dla sąsiednich wyrazów ciągu arytmetycznego (𝑎𝑛) prawdziwa jest równość:
• Wzór na 𝑛-ty wyraz ciągu geometrycznego (𝑎𝑛), określonego dla 𝑛 ≥ 1, o pierwszym wyrazie 𝑎1 i ilorazie 𝑞:
• Wzory na sumę 𝑆𝑛 początkowych 𝑛 wyrazów ciągu geometrycznego:
• Dla sąsiednich wyrazów ciągu geometrycznego (𝑎𝑛) prawdziwa jest równość:
• Suma wyrazów nieskończonego ciągu geometrycznego
Dany jest nieskończony ciąg geometryczny (𝑎𝑛), określony dla 𝑛 ≥ 1, o ilorazie 𝑞.
Niech (𝑆𝑛) oznacza ciąg sum początkowych wyrazów ciągu (𝑎𝑛), to znaczy ciąg określony wzorem 𝑆𝑛 = 𝑎1 + 𝑎2 + … + 𝑎𝑛 dla 𝑛 ≥ 1.
Jeżeli |𝑞| < 1, to ciąg (𝑆𝑛) ma granicę równą
Granicę tę nazywamy sumą wszystkich wyrazów ciągu (𝑎𝑛).
• Twierdzenie o granicy sumy, różnicy, iloczynu i ilorazu ciągów zbieżnych
Jeżeli ciągi (𝑎𝑛) i (𝑏𝑛), określone dla każdej liczby naturalnej 𝑛 ≥ 1, są zbieżne i
to ciągi
Jeżeli ponadto 𝑏𝑛 ≠ 0 dla 𝑛 ≥ 1 oraz 𝑏 ≠ 0, to ciąg
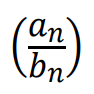
jest zbieżny i
• Twierdzenie o trzech ciągach
Jeżeli wyrazy ciągów (𝑎𝑛), (𝑏𝑛) i (𝑐𝑛), określonych dla 𝑛 ≥ 1, spełniają nierówność 𝑎𝑛 ≤ 𝑏𝑛 ≤ 𝑐𝑛 dla 𝑛 ≥ 1, a ciągi (𝑎𝑛) i (𝑐𝑛) są zbieżne do wspólnej granicy
to ciąg (𝑏𝑛) jest zbieżny, a ponadto
• Procent składany
Jeżeli kapitał początkowy 𝐾0 złożymy na okres 𝑛 lat na lokacie bankowej, której oprocentowanie wynosi 𝑝% w skali rocznej, a kapitalizacja odsetek następuje po upływie każdego roku trwania lokaty, to kapitał końcowy 𝐾𝑛 jest określony wzorem:
• Wybrane granice
⇑9. TRYGONOMETRIA
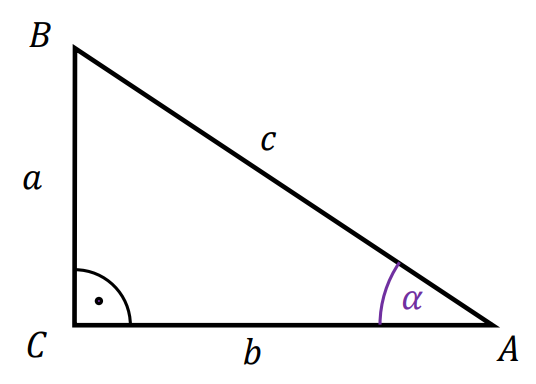
• Definicje funkcji trygonometrycznych kąta ostrego w trójkącie prostokątnym
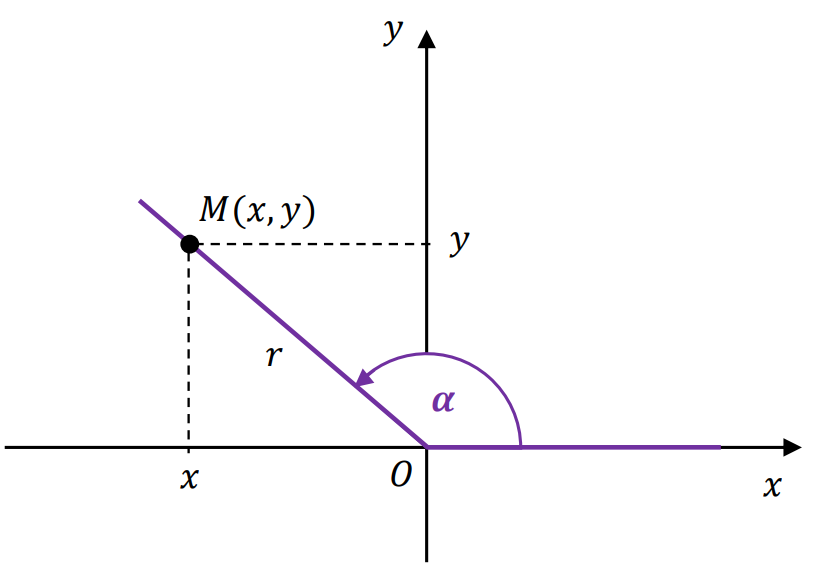
• Definicje funkcji trygonometrycznych dowolnego kąta
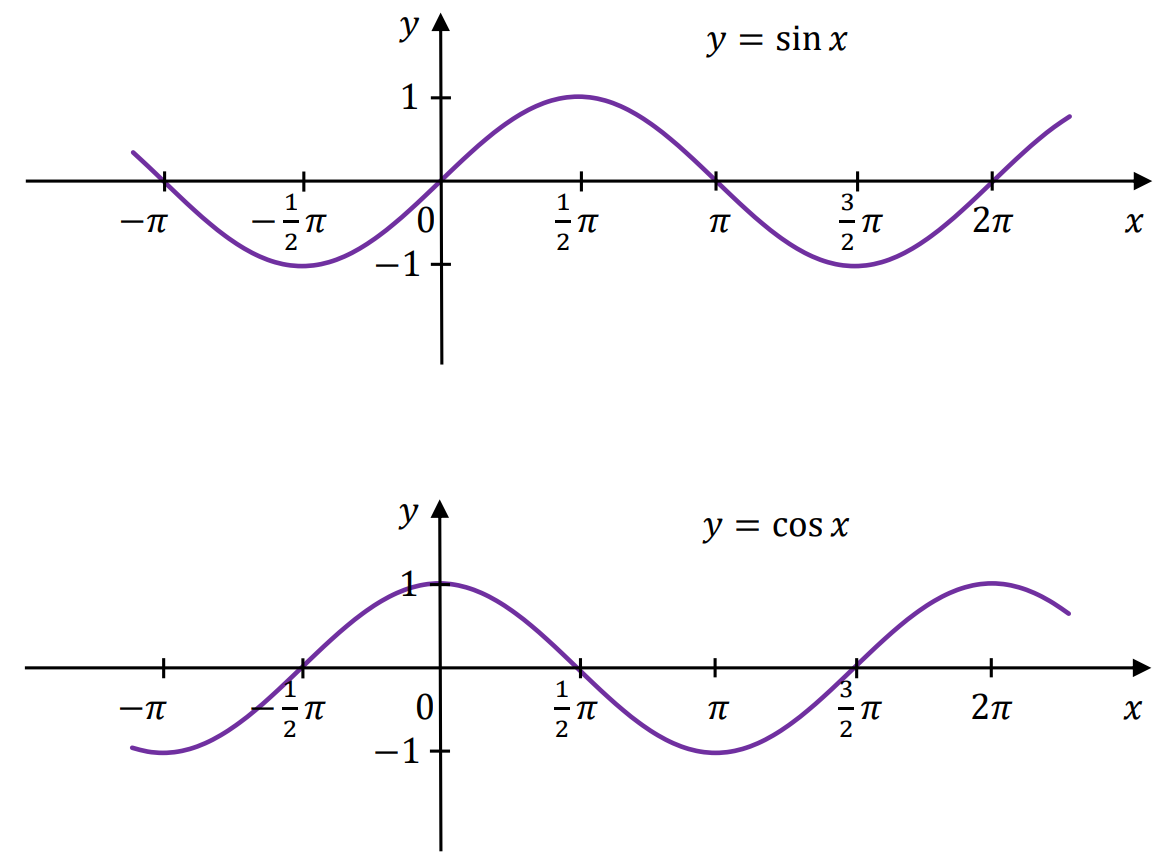
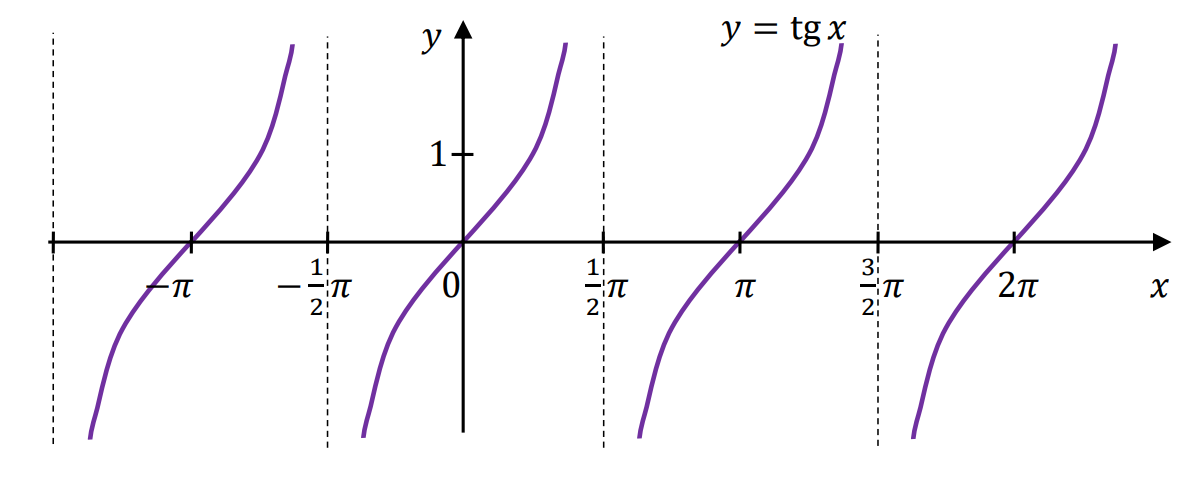
• Wykresy funkcji trygonometrycznych
• Związki między funkcjami trygonometrycznymi tego samego kąta
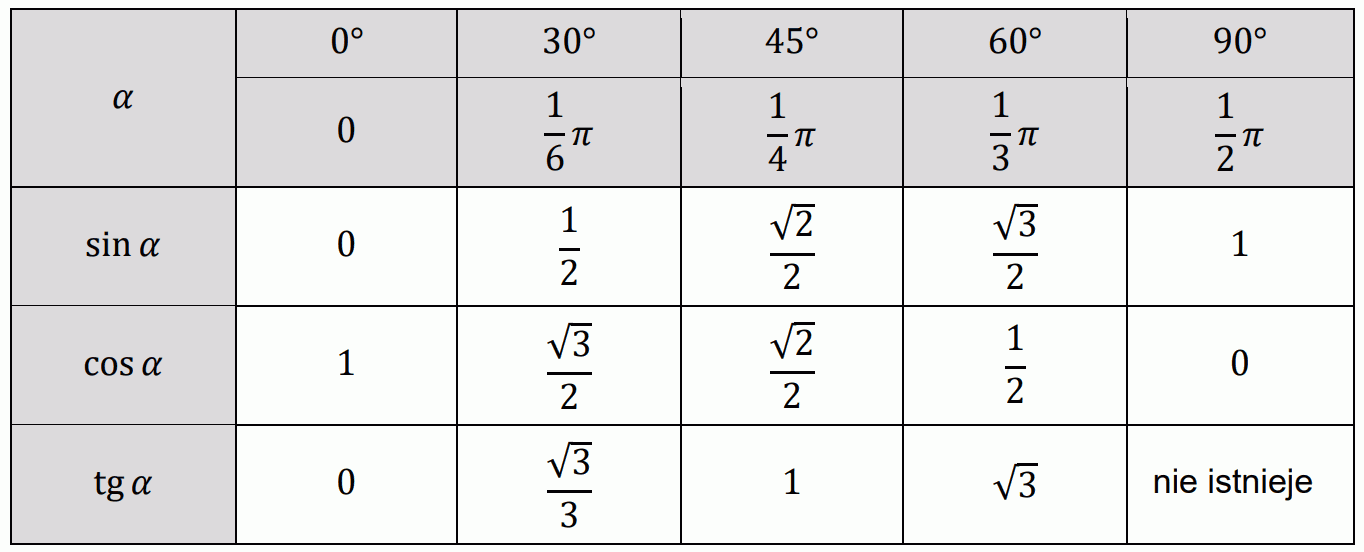
• Wartości funkcji trygonometrycznych dla wybranych kątów
• Funkcje trygonometryczne sumy i różnicy kątów
Dla dowolnych kątów 𝛼 oraz 𝛽 prawdziwe są równości:
sin(𝛼 + 𝛽) = sin 𝛼 cos 𝛽 + cos 𝛼 sin 𝛽
sin(𝛼 − 𝛽) = sin 𝛼 cos 𝛽 − cos 𝛼 sin 𝛽
cos(𝛼 + 𝛽) = cos 𝛼 cos 𝛽 − sin 𝛼 sin 𝛽
cos(𝛼 − 𝛽) = cos 𝛼 cos 𝛽 + sin 𝛼 sin 𝛽
Ponadto
• Funkcje trygonometryczne podwojonego kąta
• Wybrane wzory redukcyjne
• Sumy, różnice i iloczyny funkcji trygonometrycznych
• Okresowość funkcji trygonometrycznych
Dla każdego kąta 𝛼 i liczby całkowitej 𝑘 prawdziwe są związki:
sin(𝛼 + 𝑘 ⋅ 360°) = sin 𝛼
cos(𝛼 + 𝑘 ⋅ 360°) = cos 𝛼
Ponadto jeżeli 𝛼 ≠ 90° + 𝑚 ⋅ 180° (gdzie 𝑚 ∈ ℤ), to:
tg(𝛼 + 𝑘 ⋅ 180°) = tg 𝛼
⇑10. PLANIMETRIA
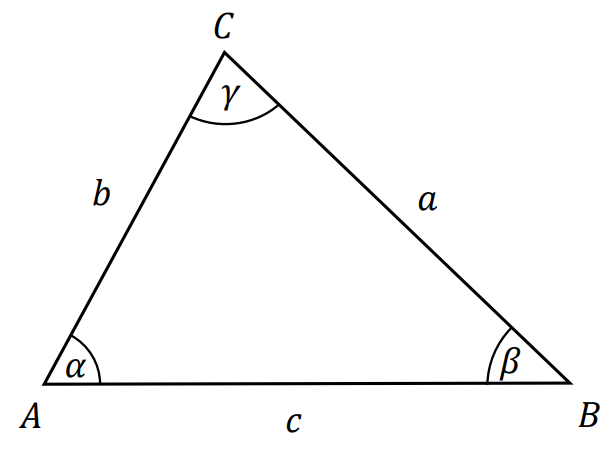
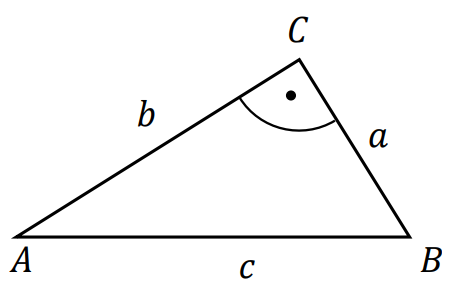
Przyjmujemy następujące oznaczenia w trójkącie 𝐴𝐵𝐶:
𝑎, 𝑏, 𝑐 – długości boków w trójkącie 𝐴𝐵𝐶
𝛼, 𝛽, 𝛾 – miary kątów wewnętrznych trójkąta leżących – odpowiednio – przy wierzchołkach 𝐴, 𝐵 oraz 𝐶
𝑅, 𝑟 – długości promieni okręgów opisanego i wpisanego w trójkąt 𝐴𝐵𝐶
ℎ𝑎, ℎ𝑏, ℎ𝑐 – wysokości trójkąta opuszczone – odpowiednio – z wierzchołków 𝐴, 𝐵 i 𝐶.
𝑝 – połowa obwodu trójkąta 𝐴𝐵𝐶, tj.
⇑• Twierdzenie Pitagorasa (wraz z twierdzeniem odwrotnym do niego)
Jeżeli w trójkącie 𝐴𝐵𝐶 kąt 𝛾 jest kątem prostym, to
𝑎² + 𝑏² = 𝑐²
Jeżeli w trójkącie 𝐴𝐵𝐶 długości boków spełniają równość 𝑎² + 𝑏² = 𝑐², to kąt 𝛾 jest kątem prostym.
⇑• Twierdzenie sinusów
⇑• Twierdzenie cosinusów
⇑• Wzory na pole trójkąta 𝐴𝐵𝐶:
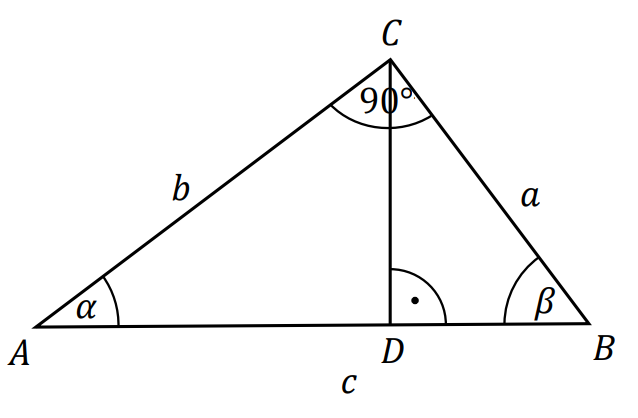
⇑• Związki miarowe w trójkącie prostokątnym
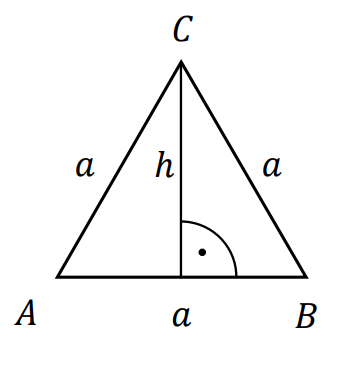
⇑• Związki miarowe w trójkącie równobocznym
𝑎 – długość boku trójkąta równobocznego
ℎ – wysokość trójkąta równobocznego
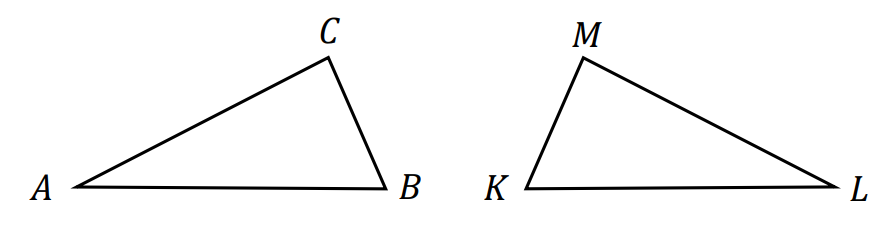
⇑• Cechy przystawania trójkątów
a) cecha przystawania „bok–bok–bok” dla trójkątów 𝐴𝐵𝐶 i 𝐾𝐿𝑀:
długości boków trójkąta 𝐴𝐵𝐶 są równe odpowiednim długościom boków trójkąta 𝐾𝐿𝑀, np.:
|𝐴𝐵| = |𝐾𝐿|, |𝐵𝐶| = |𝐾𝑀|, |𝐶𝐴| = |𝑀𝐿|.
b) cecha przystawania „bok–kąt–bok” dla trójkątów 𝐴𝐵𝐶 i 𝐾𝐿𝑀:
długości dwóch boków trójkąta 𝐴𝐵𝐶 są równe odpowiednim długościom dwóch boków trójkąta 𝐾𝐿𝑀 i kąty między tymi parami boków są przystające, np.:
|𝐴𝐵| = |𝐾𝐿|, |𝐵𝐶| = |𝐾𝑀| i |∡𝐴𝐵𝐶| = |∡𝐿𝐾𝑀|.
c) cecha przystawania „kąt–bok–kąt” dla trójkątów 𝐴𝐵𝐶 i 𝐾𝐿𝑀:
długość jednego boku trójkąta 𝐴𝐵𝐶 jest równa długości jednego boku trójkąta 𝐾𝐿𝑀 i kąty przyległe do tego boku trójkąta 𝐴𝐵𝐶 są przystające do odpowiednich kątów przyległych do odpowiedniego boku trójkąta 𝐾𝐿𝑀, np.:
|∡𝐵𝐴𝐶| = |∡𝐾𝐿𝑀| i |∡𝐴𝐵𝐶| = |∡𝐿𝐾𝑀| i |𝐴𝐵| = |𝐾𝐿|.
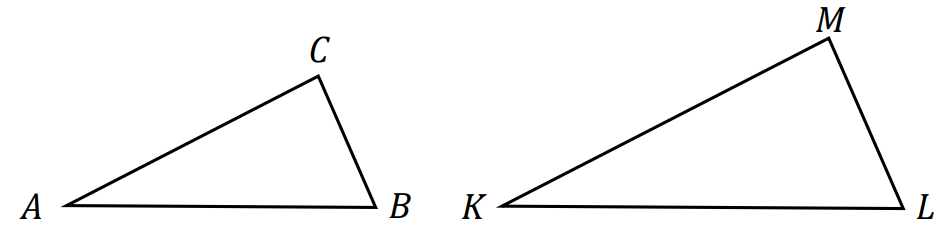
⇑• Cechy podobieństwa trójkątów
a) cecha podobieństwa „bok–bok–bok” dla trójkątów 𝐴𝐵𝐶 i 𝐾𝐿𝑀:
długości boków trójkąta 𝐴𝐵𝐶 są proporcjonalne do odpowiednich długości boków trójkąta 𝐾𝐿𝑀, np.:
b) cecha podobieństwa „bok–kąt–bok” dla trójkątów 𝐴𝐵𝐶 i 𝐾𝐿𝑀:
długości dwóch boków trójkąta 𝐴𝐵𝐶 są proporcjonalne do odpowiednich długości dwóch boków trójkąta 𝐾𝐿𝑀 i kąty między tymi parami boków są przystające, np.:
c) cecha podobieństwa „kąt–kąt–kąt” dla trójkątów 𝐴𝐵𝐶 i 𝐾𝐿𝑀:
kąty trójkąta 𝐴𝐵𝐶 są przystające do odpowiednich kątów trójkąta 𝐾𝐿𝑀, np.:
|∡𝐵𝐴𝐶| = |∡𝐿𝐾𝑀| i |∡𝐴𝐵𝐶| = |∡𝐾𝐿𝑀| i |∡𝐴𝐶𝐵| = |∡𝐾𝑀𝐿|.
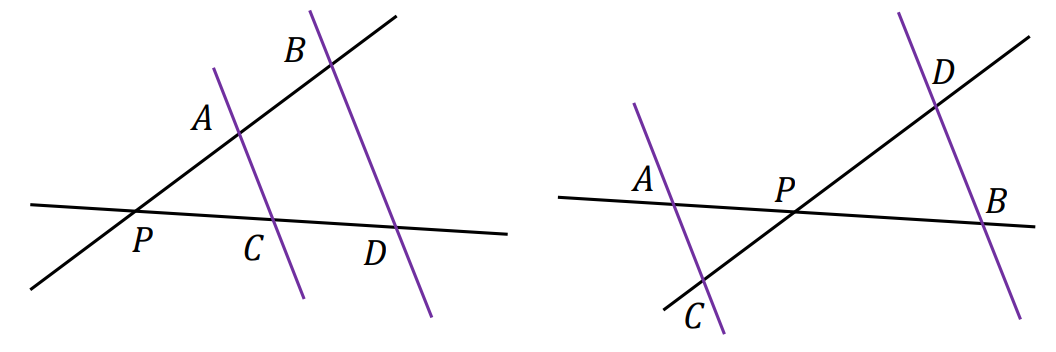
⇑• Twierdzenie Talesa (wraz z twierdzeniem odwrotnym do niego)
Różne proste 𝐴𝐵 i 𝐶𝐷 przecinają się w punkcie 𝑃, przy czym spełniony jest jeden z warunków:
– punkt 𝐴 leży wewnątrz odcinka 𝑃𝐵 oraz punkt 𝐶 leży wewnątrz odcinka 𝑃𝐷
LUB
– punkt 𝐴 leży na zewnątrz odcinka 𝑃𝐵 oraz punkt 𝐶 leży na zewnątrz odcinka 𝑃𝐷.
Jeżeli
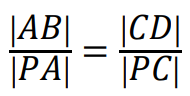
, to proste 𝐴𝐶 i 𝐵𝐷 są równoległe.
Jeżeli proste 𝐴𝐶 i 𝐵𝐷 są równoległe, to
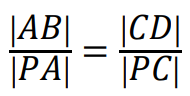
⇑• Twierdzenie o dwusiecznej kąta
Jeżeli dwusieczna kąta wewnętrznego (zewnętrznego) trójkąta 𝐴𝐵𝐶 poprowadzona z wierzchołka 𝐶 przecina prostą zawierającą odcinek 𝐴𝐵 w punkcie 𝐷, to
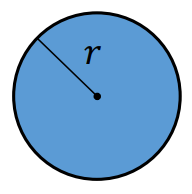
⇑• Koło
Pole 𝑃 koła o promieniu 𝑟 jest równe:
𝑃 = 𝜋𝑟²
Obwód 𝐿 koła o promieniu 𝑟 jest równy:
𝐿 = 2𝜋𝑟
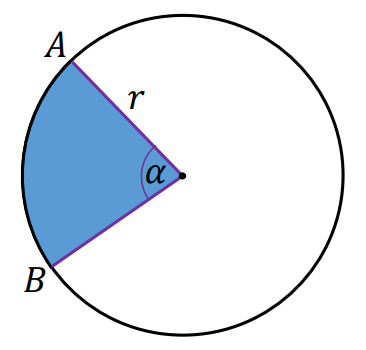
⇑• Wycinek koła
Pole 𝑃 wycinka koła o promieniu 𝑟 i kącie środkowym 𝛼 wyrażonym w stopniach jest równe:
Długość 𝐿 łuku 𝐴𝐵 wycinka koła o promieniu 𝑟 i kącie środkowym 𝛼 wyrażonym w stopniach jest równa:
⇑• Kąty w okręgu
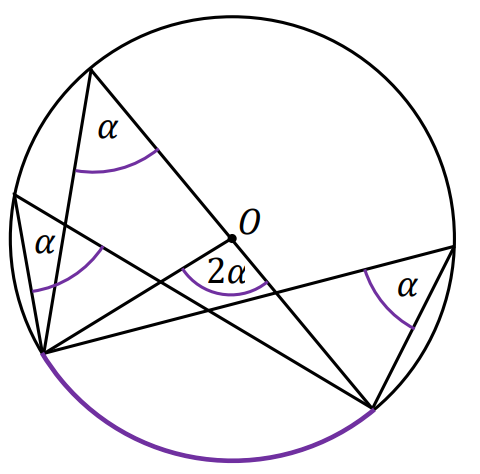
Miara kąta wpisanego w okrąg o środku 𝑂 jest równa połowie miary kąta środkowego, opartego na tym samym łuku.
W szczególności kąt wpisany oparty na półokręgu jest kątem prostym.
Miary kątów wpisanych w okrąg o środku 𝑂, opartych na tym samym łuku, są równe.
⇑• Twierdzenie o kącie między styczną i cięciwą
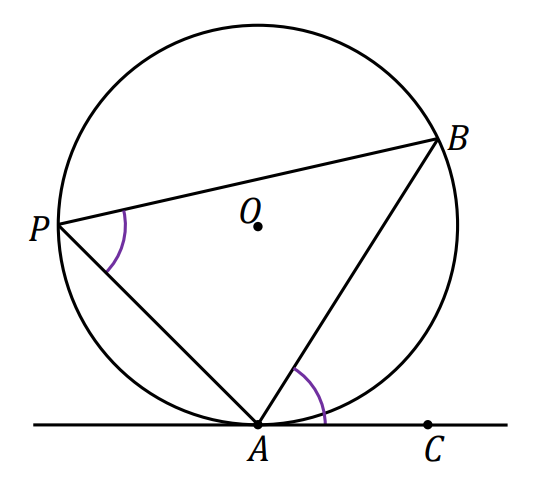
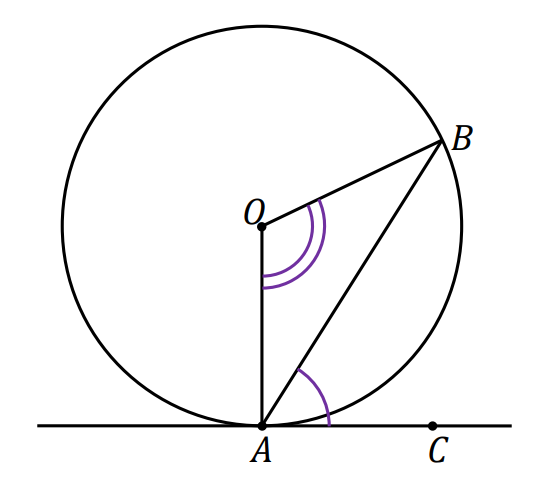
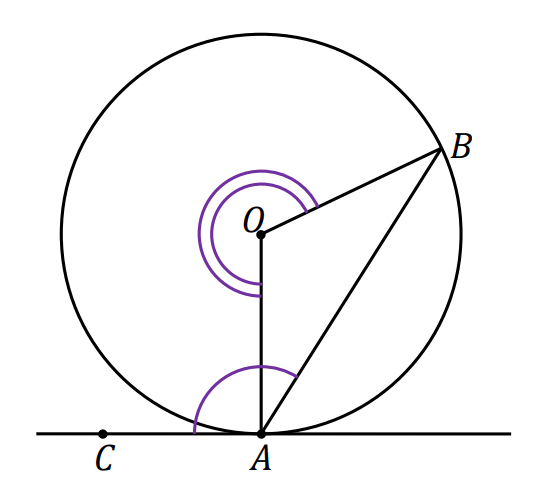
Dany jest okrąg o środku w punkcie 𝑂 i cięciwa 𝐴𝐵 tego okręgu. Prosta 𝐴𝐶 jest styczna do tego okręgu w punkcie 𝐴, natomiast punkt 𝑃 leży na tym okręgu i nie należy do kąta 𝐶𝐴𝐵. Wtedy
|∡𝐴𝑃𝐵| = |∡𝐶𝐴𝐵| i |∡𝐴𝑂𝐵| = 2 ⋅ |∡𝐶𝐴𝐵|
przy czym wybieramy ten z kątów środkowych 𝐴𝑂𝐵, który jest oparty na łuku znajdującym się wewnątrz kąta 𝐶𝐴𝐵.
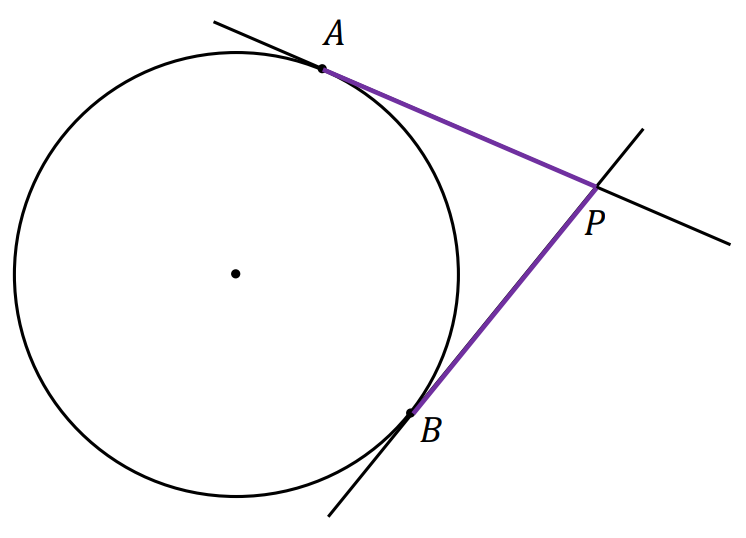
⇑• Twierdzenie o odcinkach stycznych
Jeżeli styczne do okręgu w punktach 𝐴 i 𝐵 przecinają się w punkcie 𝑃, to
|𝑃𝐴| = |𝑃𝐵|
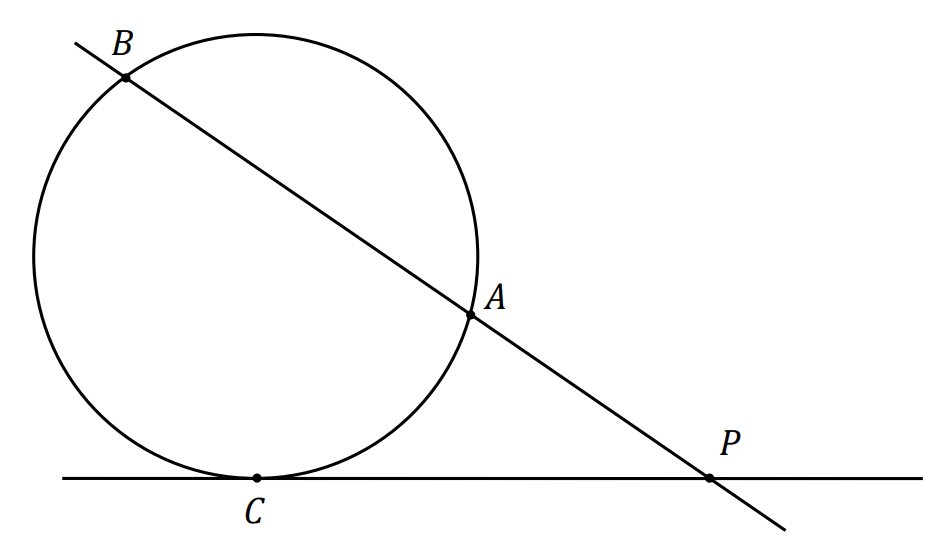
⇑• Twierdzenie o odcinkach siecznej i stycznej
Dane są: prosta przecinająca okrąg w punktach 𝐴 i 𝐵 oraz prosta styczna do tego okręgu w punkcie 𝐶. Jeżeli proste te przecinają się w punkcie 𝑃, to
|𝑃𝐴| ⋅ |𝑃𝐵| = |𝑃𝐶|²
⇑• Czworokąty
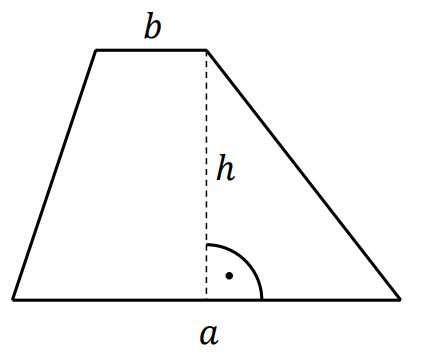
Trapez – czworokąt, który ma co najmniej jedną parę boków równoległych.
Wzór na pole 𝑃 trapezu:
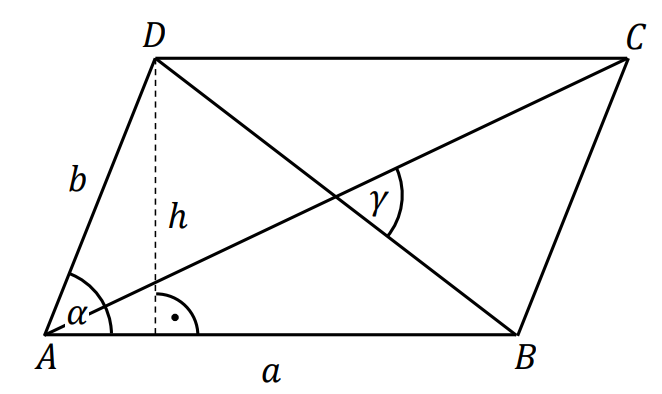
Równoległobok – czworokąt, który ma dwie pary boków równoległych.
Wzory na pole 𝑃 równoległoboku:
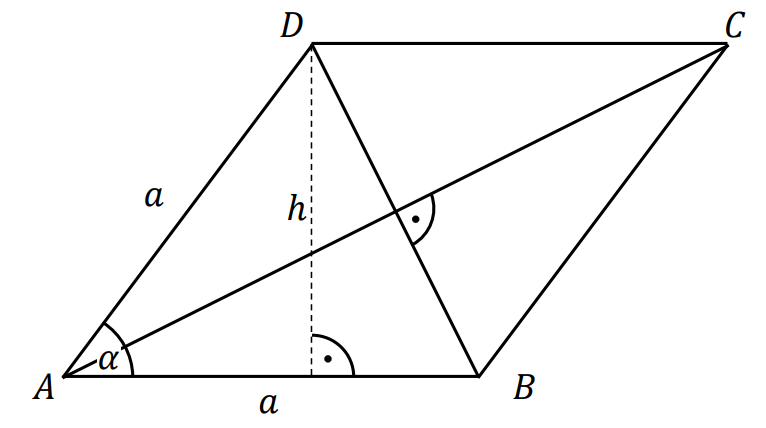
Romb – czworokąt, który ma wszystkie boki jednakowej długości.
Wzory na pole 𝑃 rombu:
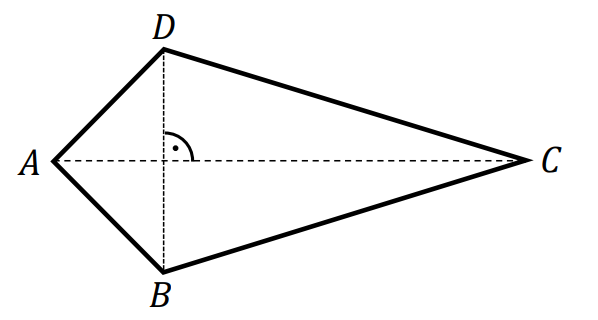
Deltoid – czworokąt wypukły, który ma oś symetrii zawierającą jedną z przekątnych.
Wzór na pole 𝑃 deltoidu:
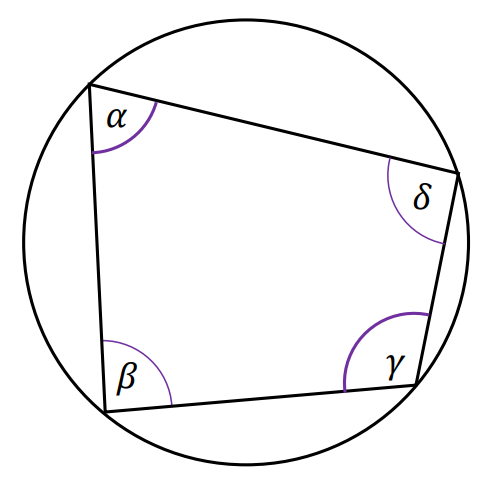
⇑• Okrąg opisany na czworokącie
Na czworokącie można opisać okrąg wtedy i tylko wtedy, gdy sumy miar jego przeciwległych kątów wewnętrznych są równe 180°.
𝛼 + 𝛾 = 𝛽 + 𝛿
𝛼 + 𝛾 = 180°
𝛽 + 𝛿 = 180°
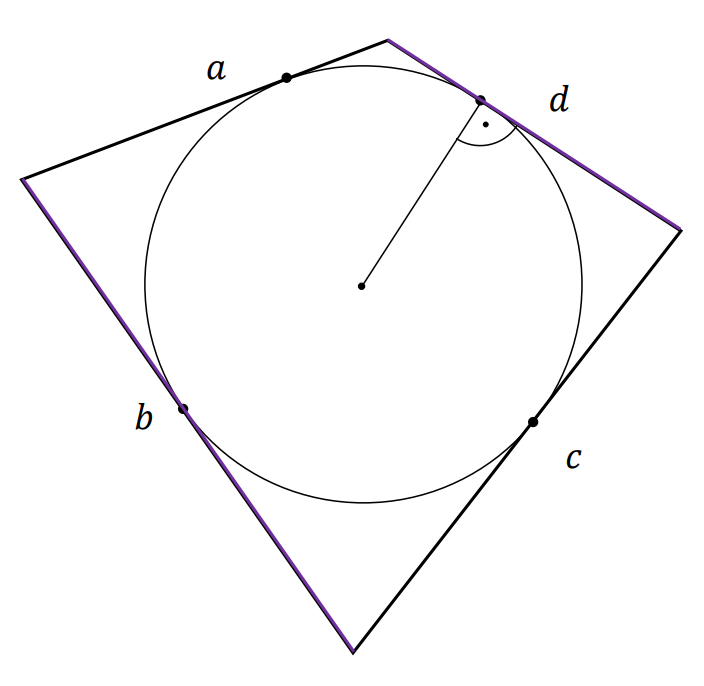
⇑• Okrąg wpisany w czworokąt
W czworokąt wypukły można wpisać okrąg wtedy i tylko wtedy, gdy sumy długości jego przeciwległych boków są równe.
𝑎 + 𝑐 = 𝑏 + 𝑑
⇑• Pola figur podobnych
Jeżeli figura ℬ o polu 𝑃ℬ jest podobna do figury 𝒜 o polu 𝑃𝒜 (różnym od zera) w skali 𝑘, to stosunek pól tych figur jest równy kwadratowi skali podobieństwa.
⇑11. GEOMETRIA ANALITYCZNA NA PŁASZCZYŹNIE KARTEZJAŃSKIEJ
⇑• Długość odcinka
Długość odcinka 𝐴𝐵 o końcach w punktach 𝐴 = (𝑥𝐴, 𝑦𝐴) oraz 𝐵 = (𝑥𝐵, 𝑦𝐵) jest równa:
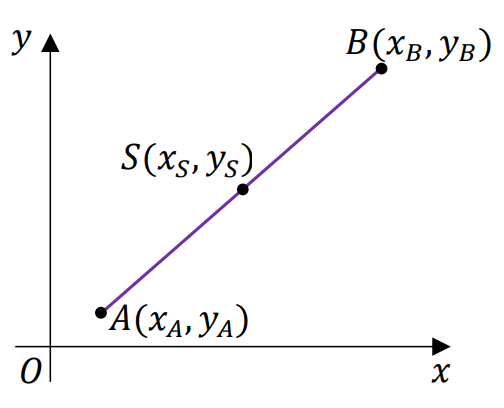
⇑• Współrzędne środka odcinka
Współrzędne środka 𝑆 = (𝑥𝑆, 𝑦𝑆) odcinka 𝐴𝐵 o końcach w punktach 𝐴 = (𝑥𝐴, 𝑦𝐴) oraz 𝐵 = (𝑥𝐵, 𝑦𝐵) są równe:
⇑• Równanie kierunkowe prostej
Jeżeli prosta nie jest równoległa do osi 𝑂𝑦, to można opisać ją równaniem kierunkowym:
𝑦 = 𝑎𝑥 + 𝑏
Liczba 𝑎 to współczynnik kierunkowy prostej.
𝑎 = tg 𝛼
Prosta o równaniu 𝑦 = 𝑎𝑥 + 𝑏 przecina oś 𝑂𝑦 w punkcie (0, 𝑏).
• Równanie kierunkowe prostej o danym współczynniku kierunkowym 𝑎, która przechodzi przez punkt 𝑃 = (𝑥0, 𝑦0):
𝑦 = 𝑎(𝑥 − 𝑥0) + 𝑦0
• Równanie kierunkowe prostej, która przechodzi przez dwa dane punkty 𝐴 = (𝑥𝐴, 𝑦𝐴) oraz 𝐵 = (𝑥𝐵, 𝑦𝐵):
𝑦 − 𝑦𝐴 = 𝑎(𝑥 − 𝑥𝐴)
gdy 𝑥𝐵 ≠ 𝑥𝐴
⇑• Równanie ogólne prostej
𝐴𝑥 + 𝐵𝑦 + 𝐶 = 0,
gdzie 𝐴, 𝐵, 𝐶 ∈ ℝ i 𝐴² + 𝐵² ≠ 0
Jeżeli 𝐴 = 0, to prosta jest równoległa do osi 𝑂𝑥; jeżeli 𝐵 = 0, to prosta jest równoległa do osi 𝑂𝑦; jeżeli 𝐶 = 0, to prosta przechodzi przez początek układu współrzędnych.
• Równanie ogólne prostej, która przechodzi przez dwa dane punkty 𝐴 = (𝑥𝐴, 𝑦𝐴) oraz 𝐵 = (𝑥𝐵, 𝑦𝐵):
(𝑦 − 𝑦𝐴)(𝑥𝐵 − 𝑥𝐴) − (𝑦𝐵 − 𝑦𝐴)(𝑥 − 𝑥𝐴) = 0
⇑• Proste równoległe
Dwie proste o równaniach kierunkowych 𝑦 = 𝑎1𝑥 + 𝑏1 oraz 𝑦 = 𝑎2𝑥 + 𝑏2 są równoległe wtedy i tylko wtedy, gdy:
𝑎1 = 𝑎2
Dwie proste o równaniach ogólnych 𝐴1𝑥 + 𝐵1𝑦 + 𝐶1 = 0 oraz 𝐴2𝑥 + 𝐵2𝑦 + 𝐶2 = 0 są równoległe wtedy i tylko wtedy, gdy:
𝐴1 ⋅ 𝐵2 − 𝐴2 ⋅ 𝐵1 = 0
⇑• Proste prostopadłe
Dwie proste o równaniach kierunkowych 𝑦 = 𝑎1𝑥 + 𝑏1 oraz 𝑦 = 𝑎2𝑥 + 𝑏2 są prostopadłe wtedy i tylko wtedy, gdy:
𝑎1 ⋅ 𝑎2 = −1
Dwie proste o równaniach ogólnych 𝐴1𝑥 + 𝐵1𝑦 + 𝐶1 = 0 oraz 𝐴2𝑥 + 𝐵2𝑦 + 𝐶2 = 0 są prostopadłe wtedy i tylko wtedy, gdy:
𝐴1 ⋅ 𝐴2 + 𝐵1 ⋅ 𝐵2 = 0
⇑• Odległość punktu od prostej
Odległość 𝑑 punktu 𝑃(𝑥0, 𝑦0) od prostej o równaniu ogólnym 𝐴𝑥 + 𝐵𝑦 + 𝐶 = 0 jest równa:
⇑• Równanie okręgu
Równanie okręgu o środku 𝑆 = (𝑎, 𝑏) i promieniu 𝑟 > 0 w postaci kanonicznej:
(𝑥 − 𝑎)² + (𝑦 − 𝑏)² = 𝑟²
Równanie okręgu o środku 𝑆 = (𝑎, 𝑏) i promieniu 𝑟 > 0 w postaci ogólnej:
𝑥² + 𝑦² − 2𝑎𝑥 − 2𝑏𝑦 + 𝑐 = 0
gdzie 𝑐 = 𝑎² + 𝑏² − 𝑟².
⇑• Współrzędne wektora, długość wektora, działania na wektorach
Dane są punkty 𝐴 = (𝑥
𝐴, 𝑦
𝐴) oraz 𝐵 = (𝑥
𝐵, 𝑦
𝐵). Współrzędne wektora
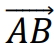
w kartezjańskim układzie współrzędnych zaczepionego w punkcie 𝐴:
Jeżeli

są wektorami oraz 𝑎 ∈ ℝ, to:
nazywamy liczbę
⇑• Przekształcenia geometryczne
Przesunięcie o wektor
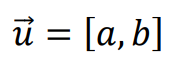
przekształca punkt 𝑃 = (𝑥, 𝑦) na punkt 𝑃’ = (𝑥 + 𝑎, 𝑦 + 𝑏).
Symetria osiowa 𝑆𝑂𝑥 względem osi 𝑂𝑥 przekształca punkt 𝑃 = (𝑥, 𝑦) na punkt 𝑃’ = (𝑥, −𝑦).
Symetria osiowa 𝑆𝑂𝑦 względem osi 𝑂𝑦 przekształca punkt 𝑃 = (𝑥, 𝑦) na punkt 𝑃’ = (−𝑥, 𝑦).
Symetria środkowa 𝑆𝐾 względem punktu 𝐾 = (𝑎, 𝑏) przekształca punkt 𝑃 = (𝑥, 𝑦) na punkt 𝑃’ = (2𝑎 − 𝑥, 2𝑏 − 𝑦).
W szczególności symetria środkowa względem początku układu współrzędnych przekształca punkt 𝑃 = (𝑥, 𝑦) na punkt 𝑃’ = (−𝑥, −𝑦).
⇑• Pole trójkąta
Pole trójkąta 𝐴𝐵𝐶 o wierzchołkach 𝐴 = (𝑥𝐴, 𝑦𝐴), 𝐵 = (𝑥𝐵, 𝑦𝐵) oraz 𝐶 = (𝑥𝐶, 𝑦𝐶) jest równe:
⇑• Współrzędne środka masy trójkąta
Współrzędne środka masy 𝑆 = (𝑥𝑆, 𝑦𝑆) trójkąta 𝐴𝐵𝐶 o wierzchołkach 𝐴 = (𝑥𝐴, 𝑦𝐴), 𝐵 = (𝑥𝐵, 𝑦𝐵) oraz 𝐶 = (𝑥𝐶, 𝑦𝐶), czyli punktu przecięcia jego środkowych:
⇑12. STEREOMETRIA
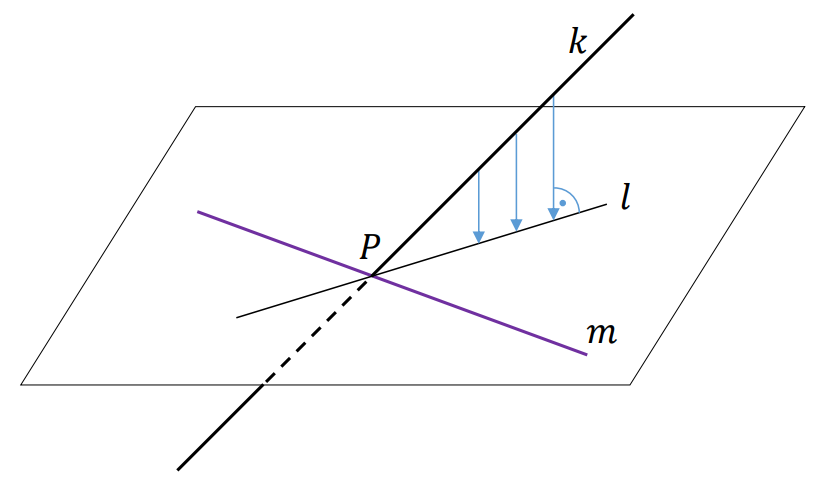
⇑• Twierdzenie o trzech prostych prostopadłych
Prosta 𝑘 przebija płaszczyznę w punkcie 𝑃 pod kątem ostrym. Prosta 𝑙 jest rzutem prostokątnym prostej 𝑘 na tę płaszczyznę. Prosta 𝑚 leży na tej płaszczyźnie i przechodzi przez punkt 𝑃.
Wówczas prosta 𝑚 jest prostopadła do prostej 𝑘 wtedy i tylko wtedy, gdy 𝑚 jest prostopadła do prostej 𝑙.
Przyjmujemy oznaczenia:
𝑃𝑐 – pole powierzchni całkowitej
𝑃𝑏 – pole powierzchni bocznej
𝑃𝑝 – pole podstawy
𝑉 – objętość
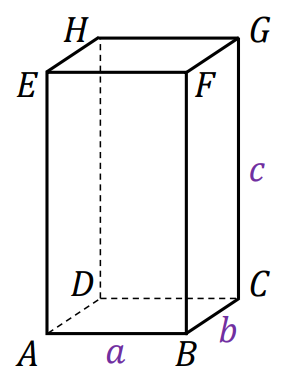
⇑• Prostopadłościan
gdzie 𝑎, 𝑏, 𝑐 są długościami krawędzi prostopadłościanu
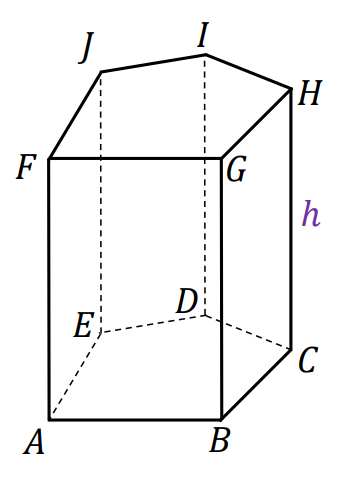
⇑• Graniastosłup prosty
gdzie 𝑂𝑏 jest obwodem podstawy graniastosłupa, natomiast ℎ – wysokością graniastosłupa.
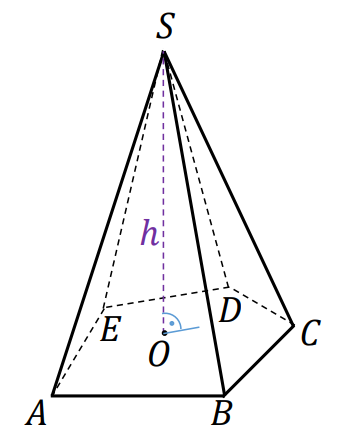
⇑• Ostrosłup
gdzie ℎ jest wysokością ostrosłupa.
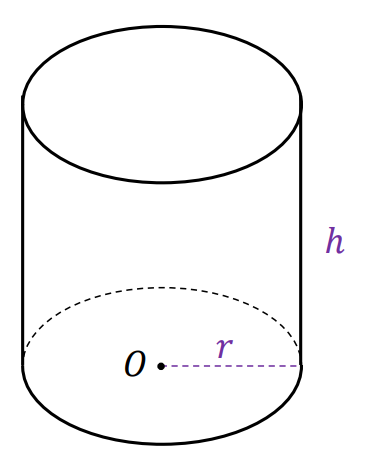
⇑• Walec
gdzie
ℎ jest wysokością walca,
𝑂 – środkiem symetrii podstawy walca,
𝑟 – promieniem podstawy walca.
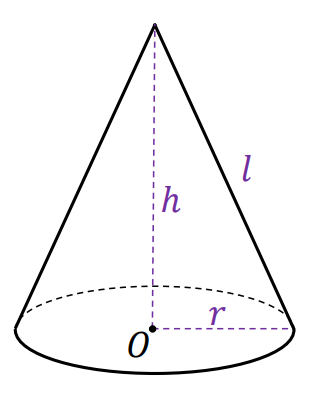
⇑• Stożek
gdzie
𝑟 jest promieniem podstawy stożka,
ℎ – jego wysokością, natomiast
𝑙 – tworzącą stożka.
Punkt 𝑂 jest środkiem symetrii podstawy stożka.
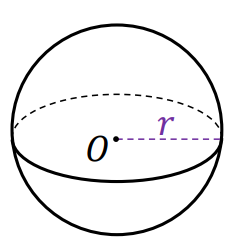
⇑• Kula
gdzie
𝑟 jest promieniem kuli,
natomiast 𝑂 – środkiem symetrii kuli.
⇑13. KOMBINATORYKA
• Permutacje
Liczba wszystkich sposobów, na które 𝑛 różnych elementów można ustawić w ciąg, jest równa 𝑛!.
• Kombinacje
Liczba wszystkich sposobów, na które spośród 𝑛 różnych elementów można wybrać 𝑘 elementów (0 ≤ 𝑘 ≤ 𝑛), jest równa
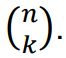
• Wariacje z powtórzeniami
Liczba wszystkich sposobów, na które z 𝑛 różnych elementów można utworzyć ciąg, składający się z 𝑘 (niekoniecznie różnych) wyrazów, jest równa 𝑛𝑘.
• Wariacje bez powtórzeń
Liczba wszystkich sposobów, na które z 𝑛 różnych elementów można utworzyć ciąg, składający się z 𝑘 różnych wyrazów (1 ≤ 𝑘 ≤ 𝑛), jest równa
⇑14. RACHUNEK PRAWDOPODOBIEŃSTWA
• Własności prawdopodobieństwa
0 ≤ 𝑃(𝐴) ≤ 1 dla każdego zdarzenia 𝐴 ⊂ Ω
𝑃(∅) = 0
𝑃(Ω) = 1
𝑃(𝐴) ≤ 𝑃(𝐵) dla każdych zdarzeń 𝐴 oraz 𝐵 takich, że 𝐴 ⊂ 𝐵 ⊂ Ω
𝑃(𝐴′) = 1 − 𝑃(𝐴) gdzie 𝐴′ oznacza zdarzenie przeciwne do zdarzenia 𝐴 ⊂ Ω
𝑃(𝐴 ∪ 𝐵) = 𝑃(𝐴) + 𝑃(𝐵) − 𝑃(𝐴 ∩ 𝐵) dla dowolnych zdarzeń 𝐴, 𝐵 ⊂ Ω
𝑃(𝐴 ∪ 𝐵) ≤ 𝑃(𝐴) + 𝑃(𝐵) dla dowolnych zdarzeń 𝐴, 𝐵 ⊂ Ω
• Twierdzenie (klasyczna definicja prawdopodobieństwa)
Niech Ω będzie skończonym zbiorem wszystkich zdarzeń elementarnych doświadczenia losowego. Jeżeli wszystkie zdarzenia jednoelementowe są jednakowo prawdopodobne, to prawdopodobieństwo zdarzenia losowego 𝐴 jest równe
gdzie |𝐴| oznacza liczbę zdarzeń elementarnych sprzyjających zdarzeniu losowemu 𝐴, natomiast |Ω| – liczbę elementów zbioru Ω.
• Schemat Bernoullego
Próbą Bernoullego nazywamy doświadczenie losowe, w którym otrzymujemy jeden z dwóch możliwych wyników. Jeden z nich nazywamy sukcesem, a drugi – porażką. Jeżeli prawdopodobieństwo sukcesu jest równe 𝑝, to prawdopodobieństwo porażki jest równe 𝑞 = 1 − 𝑝.
Schematem Bernoullego nazywamy ciąg niezależnych powtórzeń prób Bernoullego.
W schemacie Bernoullego prawdopodobieństwo 𝑃𝑛(𝑘) uzyskania w 𝑛 próbach dokładnie 𝑘 sukcesów (0 ≤ 𝑘 ≤ 𝑛) jest równe
• Prawdopodobieństwo warunkowe
Niech 𝐴, 𝐵 będą zdarzeniami losowymi zawartymi w Ω, przy czym 𝑃(𝐵) > 0.
Prawdopodobieństwem warunkowym 𝑃(𝐴|𝐵) zdarzenia 𝐴 pod warunkiem zaistnienia zdarzenia 𝐵 nazywamy liczbę
• Twierdzenie o prawdopodobieństwie całkowitym
Jeżeli zdarzenia losowe 𝐵1, 𝐵2, …, 𝐵𝑛 zawarte w Ω spełniają warunki:
1. 𝐵1, 𝐵2, …, 𝐵𝑛 są parami rozłączne,
tzn. 𝐵𝑖 ∩ 𝐵𝑗 = ∅ dla 𝑖 ≠ 𝑗, 1 ≤ 𝑖 ≤ 𝑛, 1 ≤ 𝑗 ≤ 𝑛
2. 𝐵1 ∪ 𝐵2 ∪ …∪ 𝐵𝑛 = Ω
3. 𝑃(𝐵𝑖) > 0 dla 1 ≤ 𝑖 ≤ 𝑛
to dla każdego zdarzenia losowego 𝐴 ⊂ Ω prawdziwa jest równość
• Twierdzenie Bayesa
Jeżeli zdarzenia losowe 𝐴, 𝐵1, 𝐵2, …, 𝐵𝑛 zawarte w Ω spełniają warunki:
1. 𝐵1, 𝐵2, …, 𝐵𝑛 są parami rozłączne,
tzn. 𝐵𝑖 ∩ 𝐵𝑗 = ∅ dla 𝑖 ≠ 𝑗, 1 ≤ 𝑖 ≤ 𝑛, 1 ≤ 𝑗 ≤ 𝑛
2. 𝐵1 ∪ 𝐵2 ∪ …∪ 𝐵𝑛 = Ω
3. 𝑃(𝐵𝑖) > 0 dla 1 ≤ 𝑖 ≤ 𝑛 4. 𝑃(𝐴) > 0
to dla każdego 𝑘 (1 ≤ 𝑘 ≤ 𝑛) prawdziwa jest równość
• Wartość oczekiwana zmiennej losowej
Niech 𝑋 będzie zmienną losową o wartościach 𝑥1, 𝑥2, …, 𝑥𝑛 ∈ ℝ, określoną na zbiorze Ω, przy czym 𝑃({𝜔: 𝜔 ∈ Ω oraz 𝑋(𝜔) = 𝑥𝑖}) = 𝑝𝑖 dla 1 ≤ 𝑖 ≤ 𝑛. Wartością oczekiwaną zmiennej losowej 𝑋 nazywamy liczbę
⇑15. PARAMETRY DANYCH STATYSTYCZNYCH
⇑• Średnia arytmetyczna
Średnia arytmetyczna 𝑎̅ z liczb 𝑎1, 𝑎2, …, 𝑎𝑛 jest równa:
⇑• Średnia geometryczna
Średnia geometryczna 𝑔̅ z liczb nieujemnych 𝑎1, 𝑎2, …, 𝑎𝑛 jest równa:
⇑• Średnia kwadratowa
Średnia kwadratowa z liczb 𝑎1, 𝑎2, …, 𝑎𝑛 jest równa
⇑• Nierówności między średnimi liczbowymi
Niech 𝑎1, 𝑎2, …, 𝑎𝑛 będą liczbami nieujemnymi. Wtedy (przy powyższych oznaczeniach) prawdziwe są nierówności:
Ponadto równość pomiędzy tymi średnimi liczbowymi zachodzi wtedy i tylko wtedy, gdy 𝑎1 = 𝑎2 = … = 𝑎𝑛.
⇑• Średnia ważona
Średnia ważona 𝑠̅ z liczb 𝑎1, 𝑎2, …, 𝑎𝑛, którym przypisano dodatnie wagi – odpowiednio: 𝑤1, 𝑤2, …, 𝑤𝑛, jest równa:
Medianą uporządkowanego w kolejności niemalejącej zbioru 𝑛 danych liczbowych 𝑎1, 𝑎2, …, 𝑎𝑛 jest:
– dla 𝑛 nieparzystych:
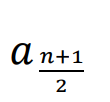
(środkowy wyraz ciągu)
– dla 𝑛 parzystych:
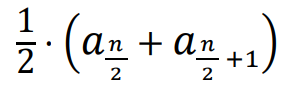
(średnia arytmetyczna dwóch środkowych wyrazów ciągu)
⇑• Wariancja i odchylenie standardowe
Wariancja 𝜎2 danych liczbowych 𝑎1, 𝑎2, …, 𝑎𝑛 o średniej arytmetycznej 𝑎̅ jest równa:
Prawdziwa jest też równość:
Odchylenie standardowe 𝜎 jest pierwiastkiem kwadratowym z wariancji:
⇑16. POCHODNA FUNKCJI
• Pochodna sumy, różnicy, iloczynu i ilorazu funkcji. Pochodna funkcji złożonej
• Pochodne wybranych funkcji
Niech 𝑎, 𝑏, 𝑐, 𝑟 będą dowolnymi liczbami rzeczywistymi.
gdzie 𝑒 jest liczbą Eulera; 𝑒 ≈ 2,72
• Równanie stycznej
Jeżeli funkcja 𝑓 ma pochodną w punkcie 𝑥0, to równanie stycznej do wykresu funkcji 𝑓 w punkcie (𝑥0, 𝑓(𝑥0)) dane jest wzorem
𝑦 = 𝑎(𝑥 − 𝑥0) + 𝑓(𝑥0)
⇑17. TABLICA WARTOŚCI FUNKCJI TRYGONOMETRYCZNYCH
α
[°]
|
sin
α
|
cos
α
|
tg
α
|
0
|
0,0000
|
1,0000
|
0,0000
|
1
|
0,0175
|
0,9998
|
0,0175
|
2
|
0,0349
|
0,9994
|
0,0349
|
3
|
0,0523
|
0,9986
|
0,0524
|
4
|
0,0698
|
0,9976
|
0,0699
|
5
|
0,0872
|
0,9962
|
0,0875
|
6
|
0,1045
|
0,9945
|
0,1051
|
7
|
0,1219
|
0,9925
|
0,1228
|
8
|
0,1392
|
0,9903
|
0,1405
|
9
|
0,1564
|
0,9877
|
0,1584
|
10
|
0,1736
|
0,9848
|
0,1763
|
11
|
0,1908
|
0,9816
|
0,1944
|
12
|
0,2079
|
0,9781
|
0,2126
|
13
|
0,2250
|
0,9744
|
0,2309
|
14
|
0,2419
|
0,9703
|
0,2493
|
15
|
0,2588
|
0,9659
|
0,2679
|
16
|
0,2756
|
0,9613
|
0,2867
|
17
|
0,2924
|
0,9563
|
0,3057
|
18
|
0,3090
|
0,9511
|
0,3249
|
19
|
0,3256
|
0,9455
|
0,3443
|
20
|
0,3420
|
0,9397
|
0,3640
|
21
|
0,3584
|
0,9336
|
0,3839
|
22
|
0,3746
|
0,9272
|
0,4040
|
23
|
0,3907
|
0,9205
|
0,4245
|
24
|
0,4067
|
0,9135
|
0,4452
|
25
|
0,4226
|
0,9063
|
0,4663
|
26
|
0,4384
|
0,8988
|
0,4877
|
27
|
0,4540
|
0,8910
|
0,5095
|
28
|
0,4695
|
0,8829
|
0,5317
|
29
|
0,4848
|
0,8746
|
0,5543
|
30
|
0,5000
|
0,8660
|
0,5774
|
31
|
0,5150
|
0,8572
|
0,6009
|
32
|
0,5299
|
0,8480
|
0,6249
|
33
|
0,5446
|
0,8387
|
0,6494
|
34
|
0,5592
|
0,8290
|
0,6745
|
35
|
0,5736
|
0,8192
|
0,7002
|
36
|
0,5878
|
0,8090
|
0,7265
|
37
|
0,6018
|
0,7986
|
0,7536
|
38
|
0,6157
|
0,7880
|
0,7813
|
39
|
0,6293
|
0,7771
|
0,8098
|
40
|
0,6428
|
0,7660
|
0,8391
|
41
|
0,6561
|
0,7547
|
0,8693
|
42
|
0,6691
|
0,7431
|
0,9004
|
43
|
0,6820
|
0,7314
|
0,9325
|
44
|
0,6947
|
0,7193
|
0,9657
|
45
|
0,7071
|
0,7071
|
1,0000
|
α
[°]
|
sin
α
|
cos
α
|
tg
α
|
45
|
0,7071
|
0,7071
|
1,0000
|
46
|
0,7193
|
0,6947
|
1,0355
|
47
|
0,7314
|
0,6820
|
1,0724
|
48
|
0,7431
|
0,6691
|
1,1106
|
49
|
0,7547
|
0,6561
|
1,1504
|
50
|
0,7660
|
0,6428
|
1,1918
|
51
|
0,7771
|
0,6293
|
1,2349
|
52
|
0,7880
|
0,6157
|
1,2799
|
53
|
0,7986
|
0,6018
|
1,3270
|
54
|
0,8090
|
0,5878
|
1,3764
|
55
|
0,8192
|
0,5736
|
1,4281
|
56
|
0,8290
|
0,5592
|
1,4826
|
57
|
0,8387
|
0,5446
|
1,5399
|
58
|
0,8480
|
0,5299
|
1,6003
|
59
|
0,8572
|
0,5150
|
1,6643
|
60
|
0,8660
|
0,5000
|
1,7321
|
61
|
0,8746
|
0,4848
|
1,8040
|
62
|
0,8829
|
0,4695
|
1,8807
|
63
|
0,8910
|
0,4540
|
1,9626
|
64
|
0,8988
|
0,4384
|
2,0503
|
65
|
0,9063
|
0,4226
|
2,1445
|
66
|
0,9135
|
0,4067
|
2,2460
|
67
|
0,9205
|
0,3907
|
2,3559
|
68
|
0,9272
|
0,3746
|
2,4751
|
69
|
0,9336
|
0,3584
|
2,6051
|
70
|
0,9397
|
0,3420
|
2,7475
|
71
|
0,9455
|
0,3256
|
2,9042
|
72
|
0,9511
|
0,3090
|
3,0777
|
73
|
0,9563
|
0,2924
|
3,2709
|
74
|
0,9613
|
0,2756
|
3,4874
|
75
|
0,9659
|
0,2588
|
3,7321
|
76
|
0,9703
|
0,2419
|
4,0108
|
77
|
0,9744
|
0,2250
|
4,3315
|
78
|
0,9781
|
0,2079
|
4,7046
|
79
|
0,9816
|
0,1908
|
5,1446
|
80
|
0,9848
|
0,1736
|
5,6713
|
81
|
0,9877
|
0,1564
|
6,3138
|
82
|
0,9903
|
0,1392
|
7,1154
|
83
|
0,9925
|
0,1219
|
8,1443
|
84
|
0,9945
|
0,1045
|
9,5144
|
85
|
0,9962
|
0,0872
|
11,4301
|
86
|
0,9976
|
0,0698
|
14,3007
|
87
|
0,9986
|
0,0523
|
19,0811
|
88
|
0,9994
|
0,0349
|
28,6363
|
89
|
0,9998
|
0,0175
|
57,2900
|
90
|
1,0000
|
0,0000
|
—
|
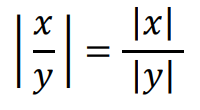
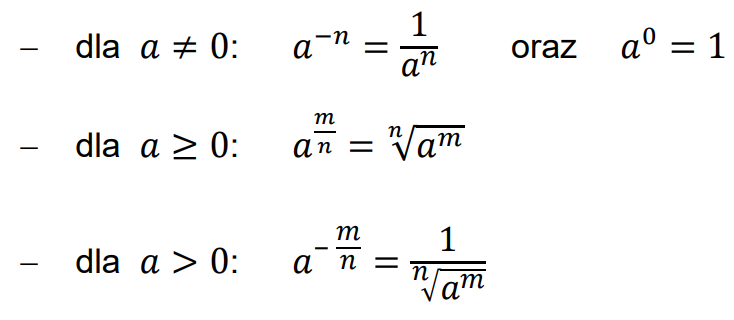
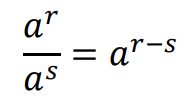
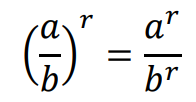
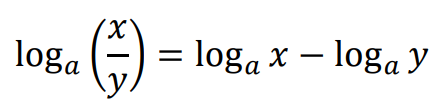
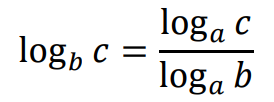
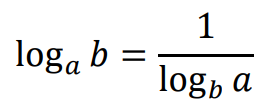
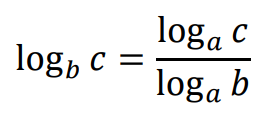
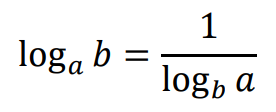
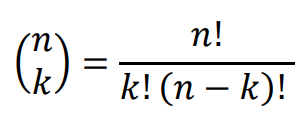
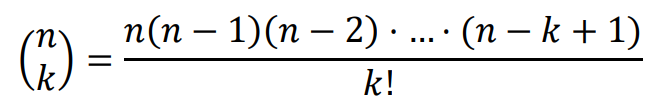
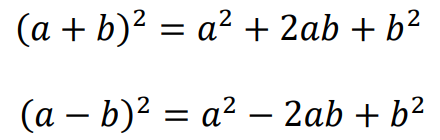
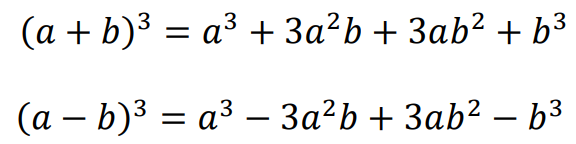
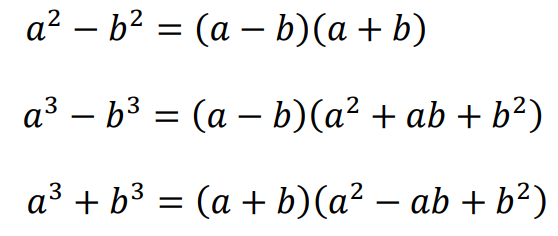
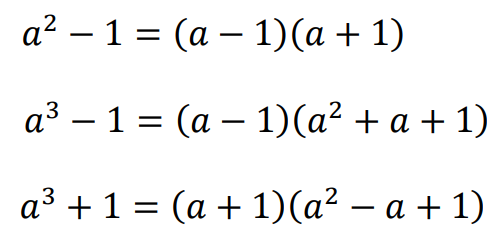
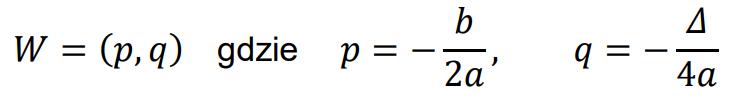
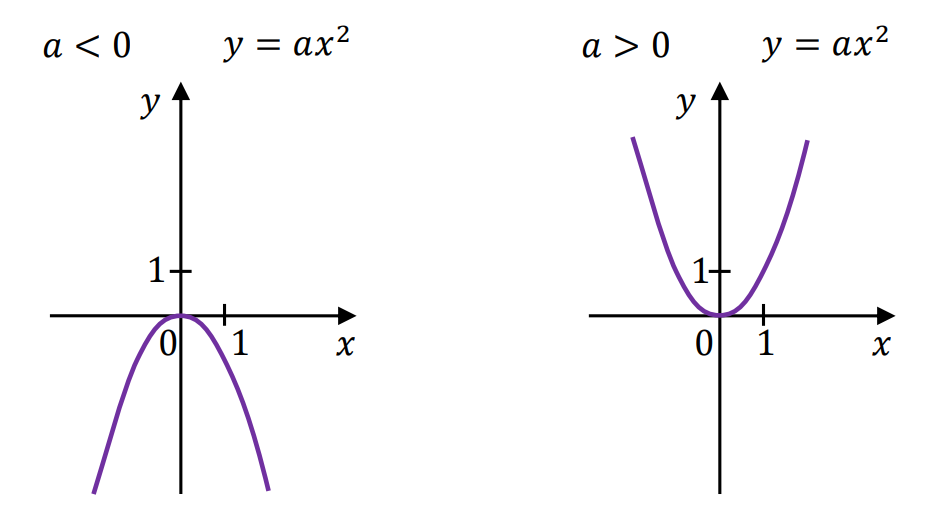
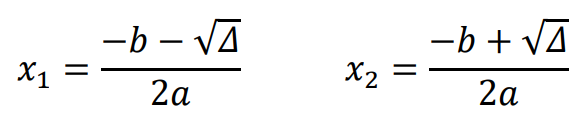
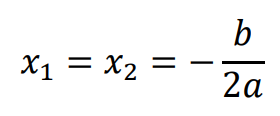
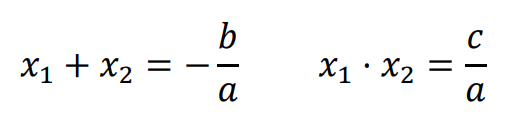
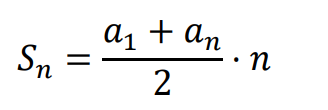
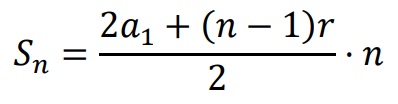
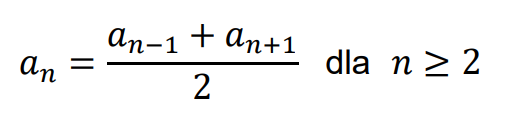
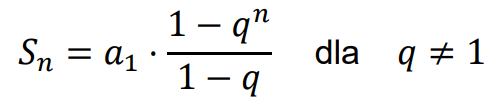
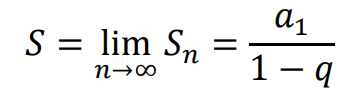
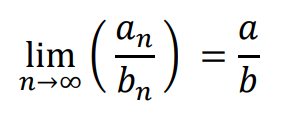
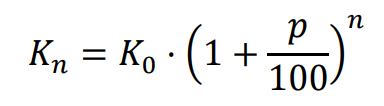
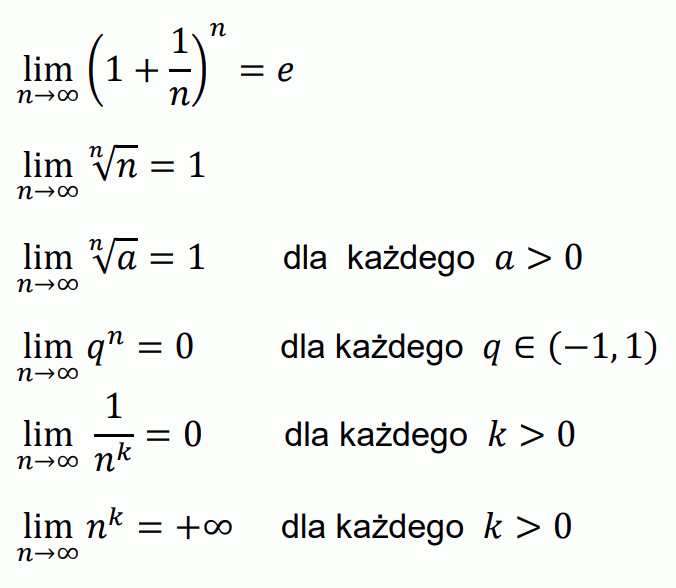
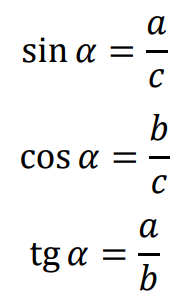
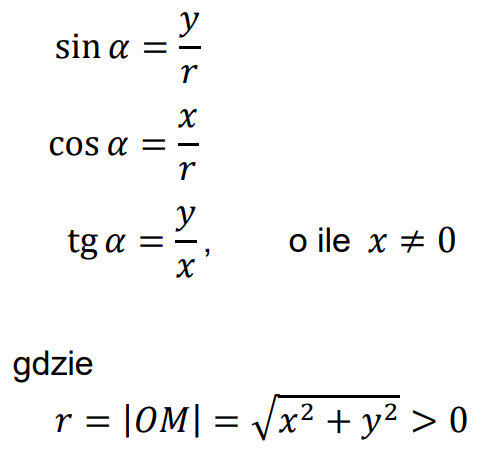
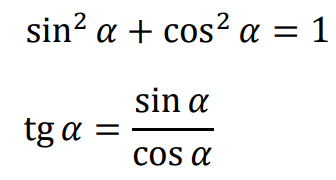
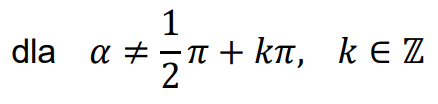
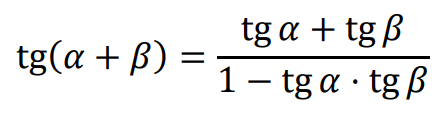
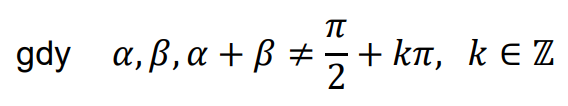
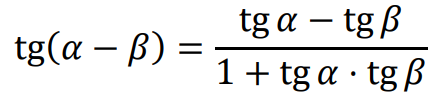
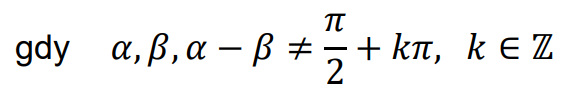
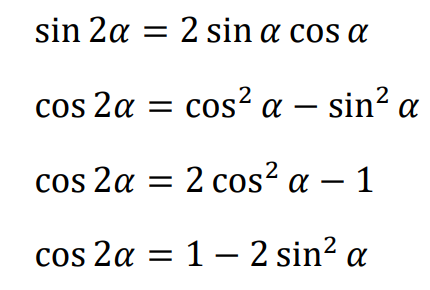
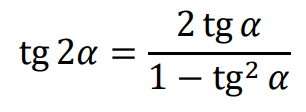
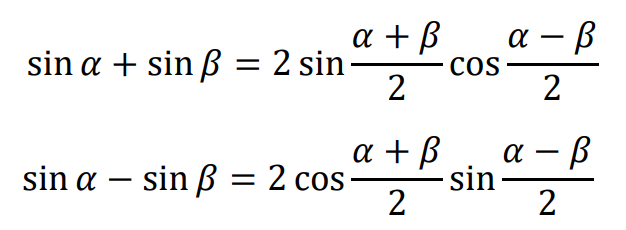
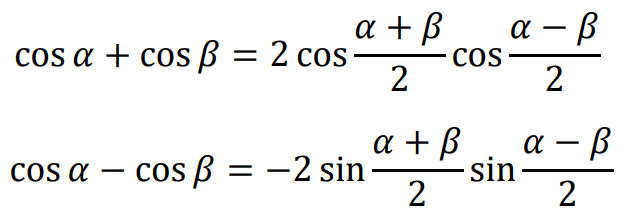
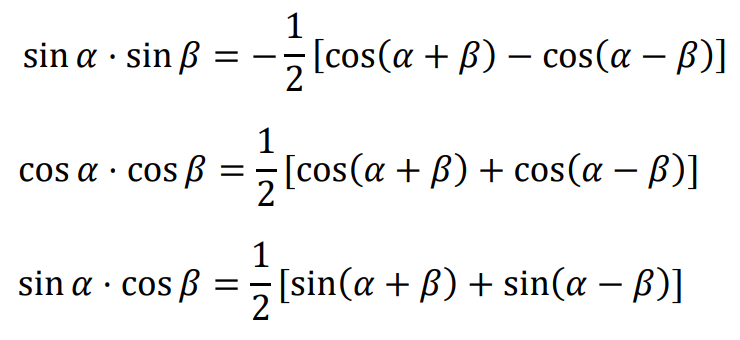
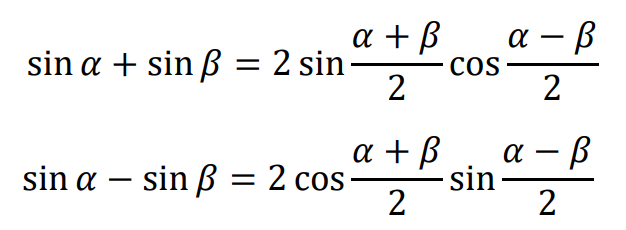
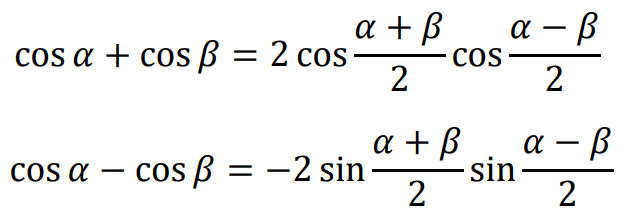
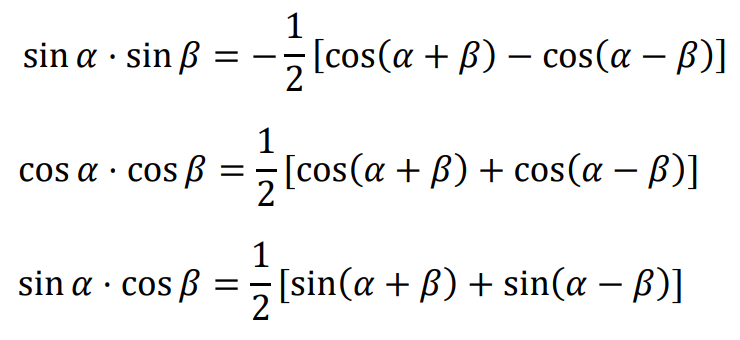
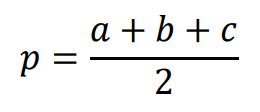
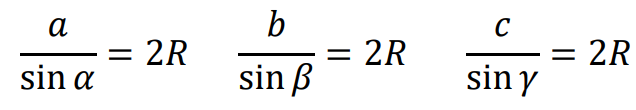
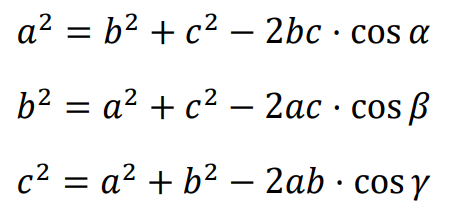
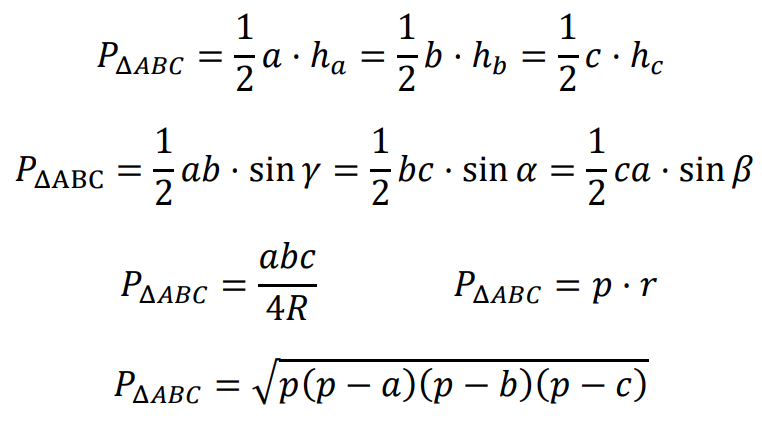
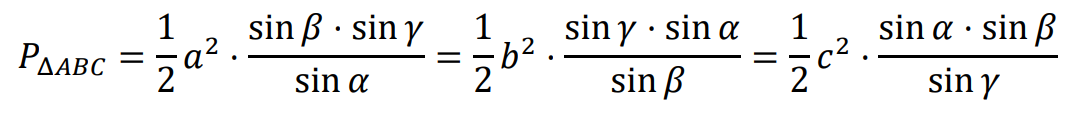
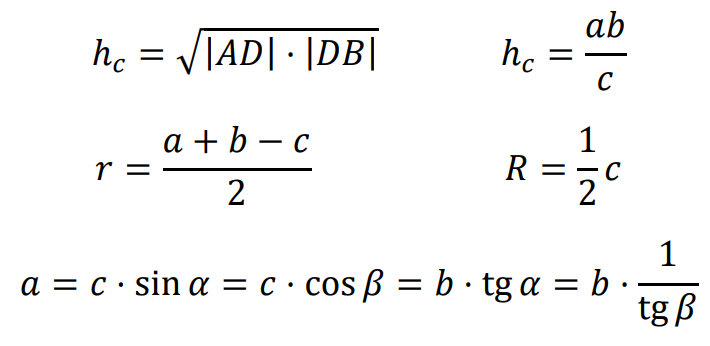
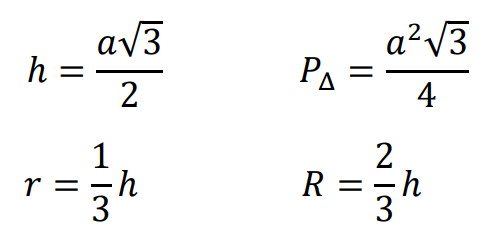
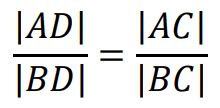
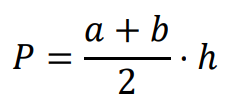
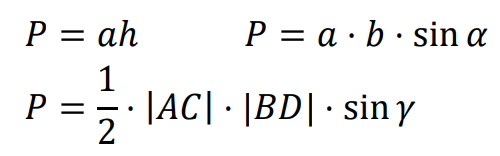
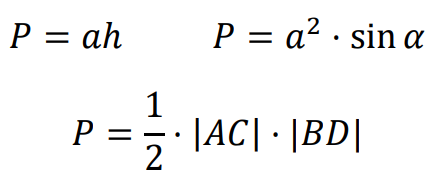
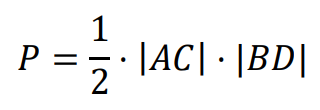
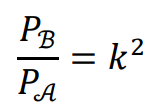

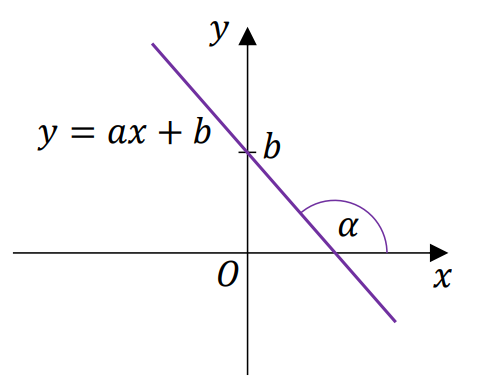
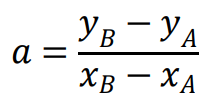
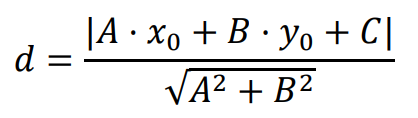
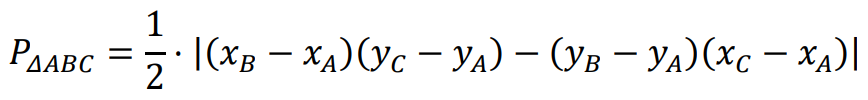
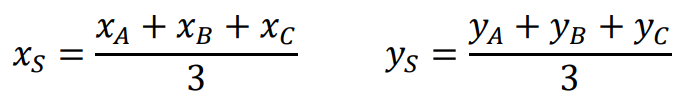
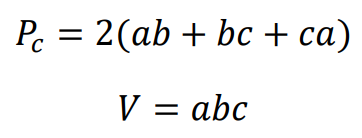
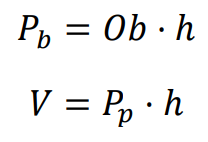
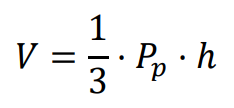
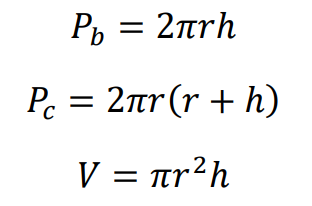
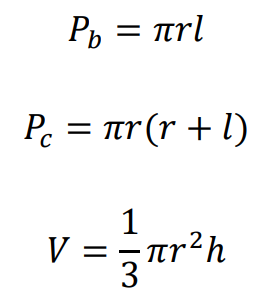
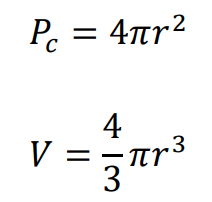
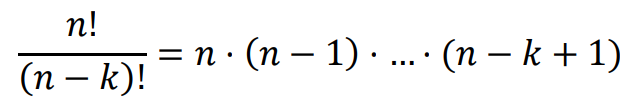
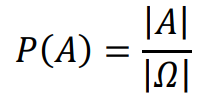
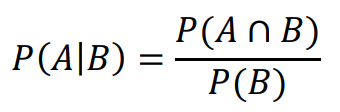
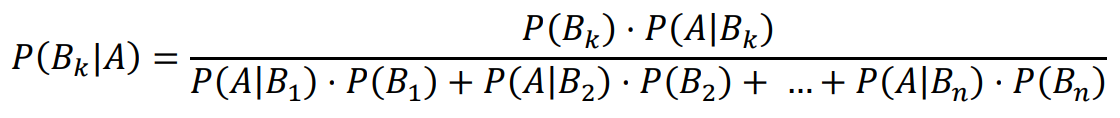
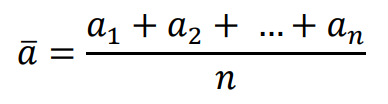
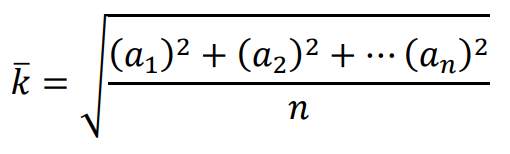
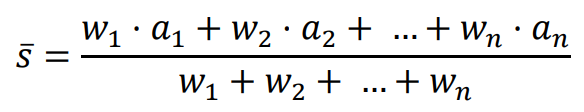
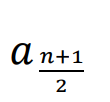 (środkowy wyraz ciągu)
(środkowy wyraz ciągu)