Odpowiedź:
Przykładowe rozwiązanie
Przyjmijmy oznaczenia jak na rysunku.
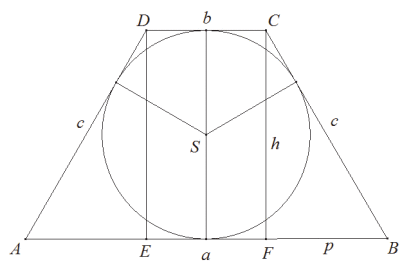
Wyznaczmy dziedzinę funkcji L. Z warunków zadania wynika, że a > h, więc a > 2 − a.
Stąd a > 1. Jeśli a = 1, to czworokąt jest kwadratem. Ponadto a < 2. Jeśli a = 2 , to h = 0 i zamiast trapezu mamy do czynienia z odcinkiem o długości 2.
Stąd a > 1. Jeśli a = 1, to czworokąt jest kwadratem. Ponadto a < 2. Jeśli a = 2 , to h = 0 i zamiast trapezu mamy do czynienia z odcinkiem o długości 2.
Rozważany trapez istnieje jedynie dla a ∈ (1,2).
Z warunków zadania otrzymujemy
a + h = 2 , skąd h = 2 − a.
Ponieważ w trapez można wpisać okrąg, więc
a + b = 2c.
a + b = 2c.
Obwód L trapezu jest więc równy
L = a + b + 2c = 2 (a + b).
L = a + b + 2c = 2 (a + b).
Trapez jest równoramienny, więc odcinki AE i FB mają tę samą długość równą
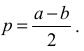
Z twierdzenia Pitagorasa dla trójkąta BCF otrzymujemy
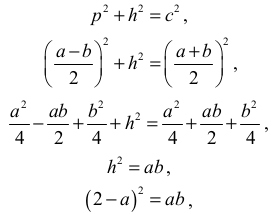
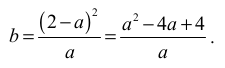
Zatem
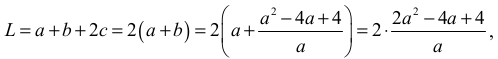
czyli

Pochodna funkcji L jest równa

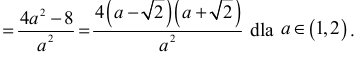
Ponieważ dla każdego a ∈ (1,2) prawdziwa jest nierówność

więc
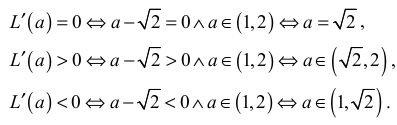
Oznacza to, że w przedziale (1,√2⟩ funkcja L jest malejąca, w przedziale ⟨√2, 2) jest
rosnąca, a w punkcie a = 2 osiąga minimum lokalne, które jest zarazem jej najmniejszą
wartością.
Tangens kąta ostrego trapezu o najmniejszym obwodzie jest równy
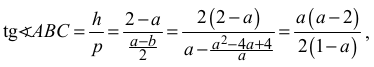
więc dla a = √2 wartość tangensa jest równa
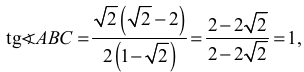
co oznacza, że ∢ ABC = 45°.
schemat punktacji
Rozwiązanie zadania składa się z trzech etapów. Ocenianie II etapu jest niezależne od wyniku
uzyskanego za I etap.

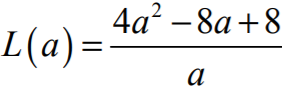
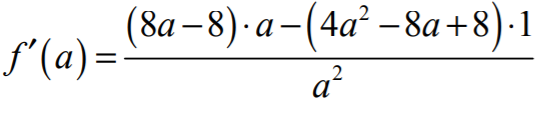 lub
lub 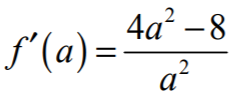
I. Pierwszy etap, który oceniamy na 3 punkty, składa się z trzech części:
I.1) wyznaczenie wszystkich wartości a, dla których istnieje trapez o podanych
własnościach, czyli dziedziny funkcji L:
DL = (1, 2)
(Za wyznaczenie dziedziny uznaje się też zapisanie dwóch nierówności:
2 – a > 0, a > 2 – a)
I.2) zapisanie poprawnej zależności między wielkościami a i b, np.:
I.3) wykazanie, że obwód L trapezu, jako funkcja zmiennej a, wyraża się wzorem:
Za poprawne rozwiązanie każdej z części tego etapu zdający otrzymuje 1 punkt.
II. Drugi etap (3 punkty) składa się z trzech części:
II.1) wyznaczenie pochodnej funkcji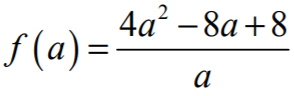 :
:
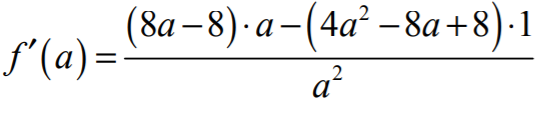 lub
lub 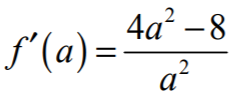
II.2) obliczenie miejsc zerowych pochodnej funkcji ƒ:
a = −√2 lub a = √2
II.3) uzasadnienie (np. badanie monotoniczności funkcji), że funkcja L posiada wartość
najmniejszą dla a = √2.
III. Trzeci etap (1 punkt) – obliczenie tangensa kąta ostrego trapezu o najmniejszym polu:
tg ∢ABC = 1.
Uwagi
1. Za poprawne uzasadnienie, że funkcja L posiada wartość najmniejszą dla wyznaczonej
wartości a, przy której pochodna się zeruje można uznać sytuacje, gdy zdający:
- opisuje, słownie lub graficznie (np. przy użyciu strzałek), monotoniczność funkcji L;
- zapisuje, że dla wyznaczonej wartości a funkcja L ma minimum lokalne i jest to
jednocześnie jej najmniejsza wartość.
Jeżeli zdający nie przedstawi takiego uzasadnienia, to za II etap może otrzymać co najwyżej
2 punkty.
2. Jeżeli zdający przyjmuje, że dziedziną funkcji L jest przedział (0,+∞) lub nie wyznaczy tej
dziedziny, to nie otrzymuje punktów za realizację części II.3.
3. Jeżeli zdający przyjmuje, że dziedziną funkcji L jest przedział (0, 2) lub zapisze warunki:
2 − a > 0 i a > 0 , to może otrzymać 1 punkt za realizację części II.3., o ile uzasadni istnienie
najmniejszej wartości funkcji.
4. Jeżeli zdający przyjmuje, że dziedziną funkcji L jest przedział (1, +∞) lub zapisze warunki:
a > h i h > 0 , lub zapisze warunek a > 2 – a, to może otrzymać 1 punkt za realizację części
II.3., o ile uzasadni istnienie najmniejszej wartości funkcji.
5. Jeżeli zdający przyjmuje, że dziedziną funkcji L jest przedział ⟨1,2), to za realizację etapu
I.1 otrzymuje 1 punkt.
6. Jeżeli zdający w wyniku błędów nie wyznaczy poprawnie długości dłużej podstawy
trapezu o najmniejszym obwodzie, ale dla wyznaczonej wartości a obliczy tangens kąta
ostrego trapezu, to może otrzymać 1 punkt za III etap.
7. Jeżeli zdający bada inną funkcję zmiennej a niż postaci 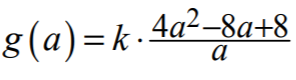 , gdzie k ≠ 0 ,
to nie otrzymuje punktów za II i III etap rozwiązania.
, gdzie k ≠ 0 ,
to nie otrzymuje punktów za II i III etap rozwiązania.
8. Jeżeli z zapisu rozwiązania wynika, że zdający stosuje poprawny wzór na pochodną ilorazu
funkcji i dalej popełnia błędy, ale otrzymana w rozwiązaniu pochodna ma dwa różne miejsca
zerowe, to zdający może otrzymać w II etapie punkty za konsekwentną realizację części II.2) i II.3). Jeżeli z zapisu rozwiązania nie wynika, że zdający stosuje poprawny wzór na
pochodną ilorazu funkcji i zdający popełnia błędy przy obliczaniu pochodnej, ale otrzymuje
wzór na pochodną, w którym w liczniku jest wielomian stopnia 2, a w mianowniku a2
, to
może w II etapie otrzymać jedynie punkt za konsekwentną realizację części II.3.