Odpowiedź:
Przykładowe rozwiązania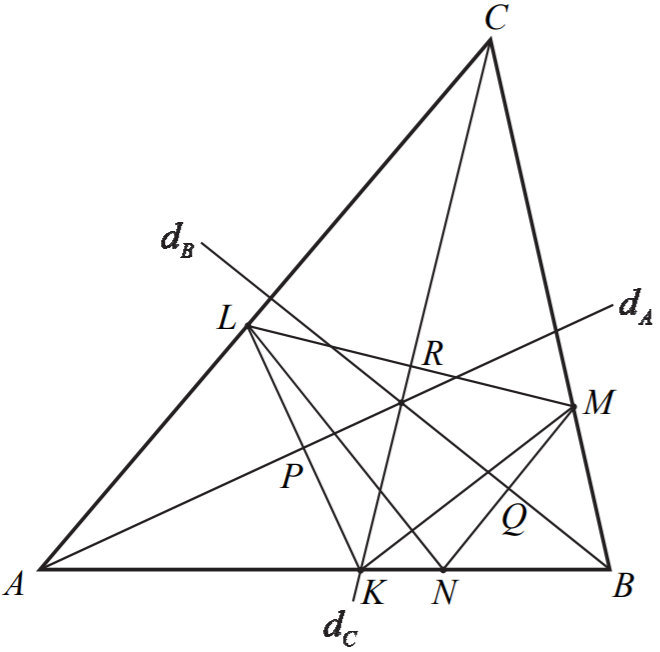
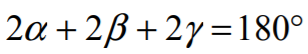
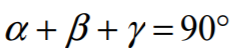
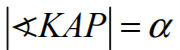
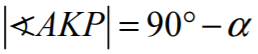
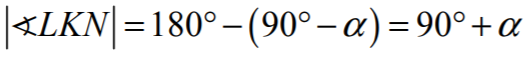

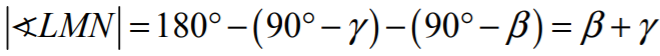
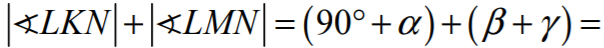
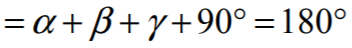

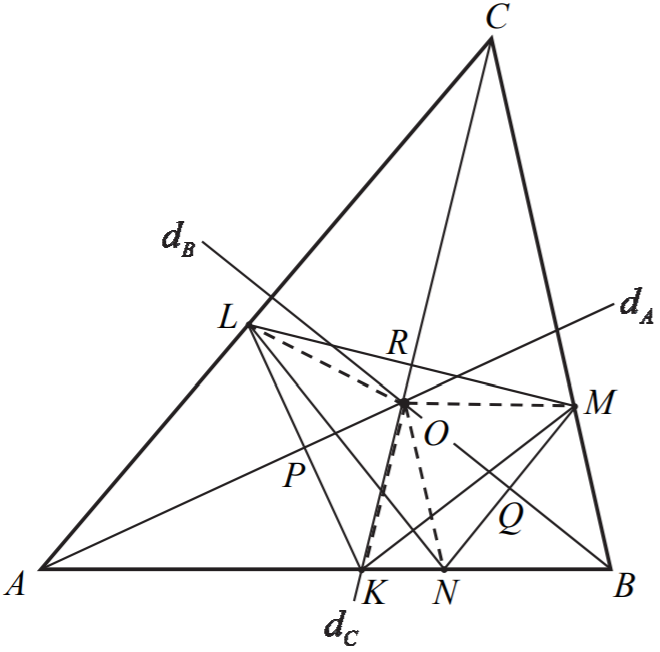
I sposób – bilans kątów
Oznaczmy miary kątów trójkąta ABC odpowiednio przez 2α, 2β, 2γ , a punkt wspólny
dwusiecznej dA i odcinka KL przez P, dwusiecznej dC i odcinka LM przez R oraz
dwusiecznej dB i odcinka MN przez Q.

Wówczas
stąd
Wtedy
zatem
i
oraz
zatem
Suma kątów LKN i LMN jest więc równa
To oznacza, że na czworokącie KNML można opisać okrąg.
II sposób – symetralne

Rozważmy trójkąt KLM.
Z definicji symetrii osiowej wynika, że dwusieczna dA jest
symetralną boku KL. Analogicznie dwusieczna dC jest symetralną boku LM.
Symetralne
boków trójkąta przecinają się w jednym punkcie, który jest środkiem okręgu opisanego na
tym trójkącie – oznaczmy go przez O.
Czyli punkt wspólny dwusiecznych dA i dC
(symetralnych boków trójkąta KLM) jest środkiem okręgu, którego promieniem jest
w szczególności odcinek OL.
Podobnie rozważmy trójkąt LMN. Z definicji symetrii osiowej wynika, że dwusieczna dC
jest symetralną boku LM . Analogicznie dwusieczna dB jest symetralną boku MN. Punkt
wspólny tych dwusiecznych (symetralnych) jest tym samym punktem, o którym była mowa
wyżej i jest oczywiście środkiem okręgu opisanego na trójkącie LMN.
Zatem musi to być ten
sam okrąg. Wszystkie wierzchołki czworokąta KNML leżą na tym okręgu.
To kończy dowód.
III sposób – równość promieni
Oznaczmy przez O punkt przecięcia się dwusiecznych kątów trójkąta ABC, punkt wspólny
dwusiecznej dA i odcinka KL przez P, dwusiecznej dC i odcinka LM przez R oraz
dwusiecznej dB i odcinka MN przez Q.

Z definicji symetrii osiowej i z treści zadania wynika, że |KP| = |LP| oraz KL ⊥ AO.
Oznacza
to, że trójkąty OPK i OPL są prostokątne, mają wspólną przyprostokątną OP oraz pozostałe
przyprostokątne są równej długości. Są to więc trójkąty przystające (na mocy cechy bkb
przystawania trójkątów).
Stąd wynika, że |OL| = |OK|. Analogicznie trójkąty ORL i ORM są
przystające oraz trójkąty OQM i OQN są przystające, a w konsekwencji |OL| = |OM| oraz |OM| = |ON|.
Zatem punkt O jest więc równooddalony od wszystkich wierzchołków
czworokąta KNML, a to oznacza, że na tym czworokącie można opisać okrąg.
schemat punktacji
Rozwiązanie, w którym jest istotny postęp 1 p.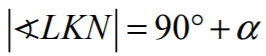
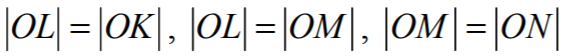
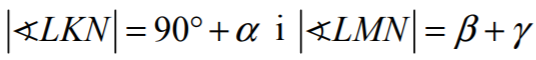


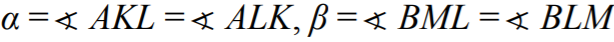 i
i 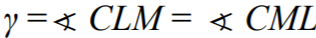
Zdający
• wyznaczy miarę jednego z kątów czworokąta KNML w zależności od miar kątów
trójkąta ABC, np.:
albo
• zapisze, że prosta zawierająca dwusieczną kąta trójkąta ABC jest symetralną jednego
z odcinków KL, LM, MN
albo
• zapisze jedną lub dwie równości spośród:
i na tym zakończy lub dalej popełnia błędy.
Pokonanie zasadniczych trudności zadania 2 p.
Zdający
• wyznaczy miary dwóch przeciwległych kątów czworokąta KNML w zależności od
miar kątów trójkąta ABC, np.:
albo
• zapisze, że punkt przecięcia dwusiecznych kątów trójkąta ABC jest środkiem okręgu
opisanego na trójkącie KLM lub na trójkącie LMN, lub że jest punktem przecięcia
symetralnych trzech boków czworokąta KNML
albo
• zapisze i uzasadni jedną lub dwie równości spośród:
Uwaga
Jeżeli zdający zapisze wszystkie równości
i stąd wyciągnie wniosek, że punkt O jest środkiem okręgu opisanego na czworokącie
KNML, ale nie uzasadni żadnej z tych równości (lub uzasadnienie nie będzie pełne),
to otrzymuje 2 punkty.
Rozwiązanie pełne 3 p.
Zdający przeprowadzi pełne rozumowanie.
Uwagi
1. Jeżeli zdający przeprowadza dowód z wykorzystaniem bilansu kątów i korzysta z równości
kątów w trójkątach równoramiennych, to może otrzymać 3 punkty także w przypadku,
gdy bez stosownego komentarza korzysta z faktu, że trójkąty są równoramienne.
2. Jeżeli zdający
• uzależni wszystkie kąty trójkąta ABC oraz jeden z kątów czworokąta KNML
albo
• uzależni jeden z kątów LKN, KNM i jeden z kątów KLM, NML
od kątów
to otrzymuje
1 punkt.
3. Jeżeli zdający
• wyznaczy 2 przeciwległe kąty czworokąta KNML w zależności od α, β, γ i wykaże, że
α + β + γ = 180º
albo
• wyznaczy wszystkie kąty czworokąta KNML i obliczy sumę dwóch przeciwległych
kątów czworokąta KNML,
to otrzymuje 2 punkty.