Odpowiedź:
Przykładowe rozwiązanie
I sposób
Zaznaczmy na rysunku kąt α – kąt nachylenia ściany bocznej do płaszczyzny podstawy i wprowadzamy następujące oznaczenia:
a – krawędź podstawy ostrosłupa,
h – wysokość ostrosłupa.
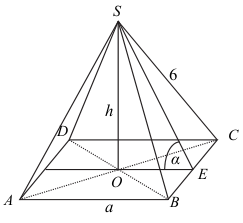
Korzystając z definicji tangensa kąta ostrego w trójkącie prostokątnym SOE otrzymujemy związek
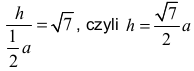
Z twierdzenia Pitagorasa w trójkącie SOC wynika równanie
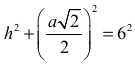
Wykorzystując wcześniejszą zależność otrzymujemy
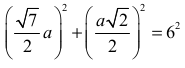
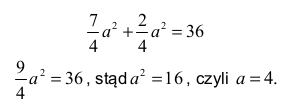
Stąd
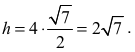
Obliczamy objętość ostrosłupa:
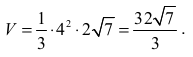
II sposób
Zaznaczmy na rysunku kąt α – kąt nachylenia ściany bocznej do płaszczyzny podstawy i wprowadzamy następujące oznaczenia:
a – krawędź podstawy ostrosłupa,
h – wysokość ostrosłupa,
hb – wysokość ściany bocznej ostrosłupa

Korzystając z definicji tangensa kąta ostrego w trójkącie prostokątnym SOE otrzymujemy:
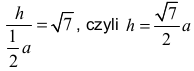
Z twierdzenia Pitagorasa w trójkącie prostokątnym SEC otrzymujemy
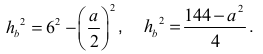
Z twierdzenia Pitagorasa w trójkącie prostokątnym SOE otrzymujemy
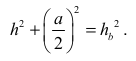
Zatem
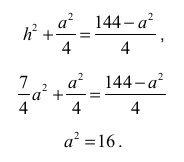
Stąd a = 4 , więc h = 2√7 .
Objętość ostrosłupa jest równa:
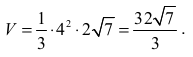
schemat punktacji
Rozwiązanie, w którym postęp jest niewielki, ale konieczny na drodze do pełnego
rozwiązania 1 p.
Zdający
• zaznaczy na rysunku kąt α nachylenia ściany bocznej do płaszczyzny podstawy
albo
• zapisze równanie wynikające z definicji tangensa kąta α:
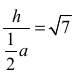
albo
• zapisze równanie wynikające z twierdzenia Pitagorasa w trójkącie SOE:
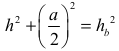
albo
• zapisze równanie wynikające z twierdzenia Pitagorasa w trójkącie SEC:
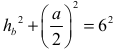
albo
• zapisze równanie wynikające z twierdzenia Pitagorasa w trójkącie SOC:
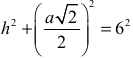
albo
• zapisze równanie wynikające z definicji sinusa kąta α:
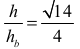
albo
• zapisze równanie wynikające z definicji cosinusa kąta α :
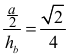
i na tym zakończy lub dalej popełni błędy.
Rozwiązanie, w którym jest istotny postęp 2 p.
Zdający zapisze
• układ dwóch równań z dwiema niewiadomymi, np.:
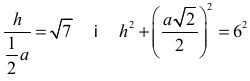
lub
• układ trzech równań z trzema niewiadomymi, np.:
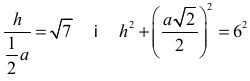
i na tym zakończy lub dalej popełni błędy.
Pokonanie zasadniczych trudności zadania 3 p.
Zdający zapisze równanie z jedną niewiadomą, np.:
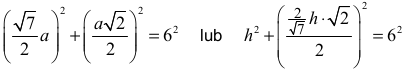
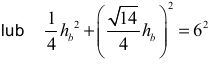
i na tym zakończy lub dalej popełni błędy.
Rozwiązanie prawie pełne 4 p.
Zdający:
• obliczy długość krawędzi podstawy ostrosłupa lub wysokość ostrosłupa: a = 4 , h = 2√7
albo
• obliczy wysokość hb ściany bocznej ostrosłupa oraz wyznaczy objętość ostrosłupa w zależności od tej wysokości:
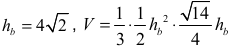
i na tym zakończy lub dalej popełni błędy
Rozwiązanie pełne 5 p.
Zdający obliczy objętość ostrosłupa:
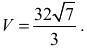
Uwagi
1. Jeśli zdający popełni błędy rachunkowe, które nie przekreślają poprawności rozumowania i konsekwentnie rozwiąże zadanie do końca, to może otrzymać za całe rozwiązanie co najwyżej 4 punkty.
2. Jeżeli jedynym błędem zdającego jest pominięcie współczynnika 1⁄3 we wzorze na objętość ostrosłupa, to otrzymuje 4 punkty.
3. Jeżeli jedynym błędem jest:
a) zastosowanie niepoprawnej definicji tangensa (lub niepoprawnej definicji innej
funkcji trygonometrycznej wykorzystanej przez zdającego), np.
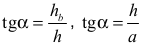
b) niepoprawne zastosowanie twierdzenia Pitagorasa,
c) błąd polegający na zastosowaniu niepoprawnego wzoru
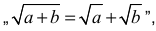
to zdający może otrzymać co najwyżej 3 punkty za całe rozwiązanie, o ile nie popełnia innych błędów i konsekwentnie rozwiąże zadanie do końca.
4. Jeżeli zdający popełnia jeden błąd, opisany w uwadze 3., a ponadto popełnia błędy rachunkowe, ale poprawnie realizuje strategię rozwiązania, to otrzymuje co najwyżej 2 punkty za całe rozwiązanie.
5. Jeżeli zdający błędnie interpretuje kąt między ścianą boczną i płaszczyzną podstawy tego ostrosłupa, to otrzymuje co najwyżej 1 punkt za całe rozwiązanie, o ile poprawnie zastosuje twierdzenie Pitagorasa.
6. Jeżeli zdający przyjmuje, że krawędź podstawy ostrosłupa jest równa 6, to może otrzymać co najwyżej 1 punkt za całe rozwiązanie, o ile zapisze poprawny związek między wielkościami h, hb i a lub zaznaczy poprawnie kąt nachylenia ściany bocznej ostrosłupa do płaszczyzny podstawy.
7. Akceptujemy poprawne przybliżenia liczb rzeczywistych.