Przykładowe rozwiązania
I sposób
Przekształcamy równoważnie nierówność i otrzymujemy kolejno:
a2 - 2ab + 2b2 > 0 ,
a2 - 2ab + b2 + b2 > 0 ,
(a - b )2 + b2 > 0 .
Nierówność (a - b)2 + b2 > 0 jest prawdziwa, ponieważ:
1) wyrażenie (a - b)2 jest dodatnie, gdyż z założenia wynika a - b ≠ 0 i kwadrat każdej liczby rzeczywistej różnej od zera jest dodatni,
2) wyrażenie b2 jest nieujemne,
3) suma dwóch liczb rzeczywistych, z których jedna jest liczbą dodatnią, a druga liczbą nieujemną, jest liczbą dodatnią.
II sposób
Przekształcamy równoważnie nierówność i otrzymujemy:
a2 - 2ab + 2b2 > 0 .
Wyrażenie a2 - 2ab + 2b2 traktujemy jako trójmian kwadratowy jednej zmiennej np. a.
Wyróżnik trójmianu kwadratowego
a2 - 2ab + 2b2
jest równy:
Δ = 4b2 - 8b2 = - 4b2.
Ten wyróżnik jest niedodatni dla każdej rzeczywistej wartości b.
Gdy Δ < 0, to a2 - 2ab + 2b2 > 0 dla każdej rzeczywistej wartości a.
Gdy Δ = 0, to b = 0, stąd a2 > 0, ponieważ z założenia a ≠ b.
Oznacza to, że dla każdych dwóch różnych liczb rzeczywistych a i b prawdziwa jest nierówność
a2 - 2ab + 2b2 > 0 .
III sposób
Przekształcamy równoważnie nierówność
a (a - 2b) + 2b2 > 0 i otrzymujemy:
a2 - 2ab + 2b2 > 0 .
Z założenia wynika, że liczby a i b nie mogą jednocześnie przyjmować wartości 0 .
Jeżeli b ≠ 0, to b2 > 0. Dzielimy obie strony nierówności przez b2 i otrzymujemy nierówność równoważną
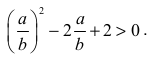
Niech x = a/b.
Otrzymujemy nierówność kwadratową
x2 - 2x + 2 > 0 z niewiadomą x .
Zauważamy, że ta nierówność jest prawdziwa dla każdej liczby rzeczywistej x , bo z równości
x2 - 2x + 2 = (x-1)2 +1
wnioskujemy, że
(x-1)2 +1 > 0,
wobec oczywistej nierówności
(x-1)2 ≥ 0.
Natomiast jeżeli a ≠ 0, to a2 > 0.
Dzielimy obie strony nierówności przez a2 i otrzymujemy nierówność równoważną
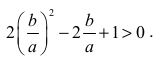
Niech teraz x = b/a.
Otrzymujemy nierówność kwadratową
2x2 -2x +1 > 0 z niewiadomą x.
Ponieważ wyróżnik trójmianu
2x2 - 2x +1
jest ujemny oraz współczynnik przy najwyższej potędze trójmianu jest dodatni, więc ten trójmian przyjmuje tylko wartości dodatnie dla każdej liczby rzeczywistej x.
Z rozważonych przypadków wynika, że nierówność jest prawdziwa dla każdych dwóch różnych liczb rzeczywistych a i b.
To kończy dowód.
IV sposób
Niech a ≠b. Rozważmy następujące przypadki:
Przypadek I: a · b > 0 .
Przekształcamy równoważnie nierówność
a(a - 2b) + 2b2 > 0
i otrzymujemy:
a2 + 2b2 - 2√2 ab > 2ab - 2√2 ab .
Stąd (a-√2 b)2 > 2ab (l - √2).
Wyrażenie (a -√2 b)2 jest nieujemne.
Wyrażenie 2ab (l -√2) jest ujemne,
ponieważ i - √2 < 0 i z założenia ab > 0.
Nierówność jest prawdziwa dla każdych dwóch liczb rzeczywistych a i b, takich, że
a · b > 0 i a ≠b .
Przypadek II: a · b < 0.
Przekształcamy równoważnie nierówność
a (a - 2b) + 2b2 > 0
i otrzymujemy:
a2 + 2b2 + 2√2 ab > 2ab + 2√2 ab .
Stąd (a + √2 b)2 > 2ab (l + √2).
Wyrażenie (a+√2 b)2 jest nieujemne.
Wyrażenie 2ab (l + √2) jest ujemne, ponieważ
1 + √2 > 0 i z założenia ab < 0 .
Nierówność jest prawdziwa dla każdych dwóch liczb rzeczywistych a i b, takich, że
a · b < 0 i a ≠ b .
Przypadek III: a · b = 0
Przekształcamy równoważnie nierówność
a(a - 2b) + 2b2 > 0 i otrzymujemy:
a2 - 2ab + 2b2 > 0.
Ponieważ a · b = 0,
więc nierówność a2 - 2ab + 2b2 > 0 możemy zapisać w postaci
a2 + 2b2 > 0.
Suma kwadratów dwóch dowolnych liczb rzeczywistych a i b, takich, że a ≠ b jest dodatnia.
Nierówność jest prawdziwa dla każdych dwóch liczb rzeczywistych a i b, takich, że
a · b = 0 i a ≠b .
To kończy dowód.
V sposób (dowód nie wprost)
Załóżmy, że istnieją różne liczby rzeczywiste a i b, dla których prawdziwa jest nierówność
a (a - 2b) + 2b2 ≤ 0.
Powyższa nierówność jest równoważna nierównościom:
a2 - 2ab + 2b2 ≤ 0,
(a - b)2 + b2 ≤ 0.
Ponieważ lewa strona tej nierówności jest sumą dwóch liczb nieujemnych
(a - b)2 i b2,
więc może zachodzić jedynie przypadek
(a - b)2 + b2 = 0.
Wynika stąd, że a - b = 0 i b = 0.
Zatem a = 0 i b = 0, co przeczy założeniu, że liczby a i b są różne.
Otrzymana sprzeczność oznacza, że nierówność
a (a - 2b) + 2b2 < 0 jest fałszywa.
Prawdziwa zatem jest nierówność
a(a - 2b) + 2b2 > 0, dla każdych dwóch różnych liczb rzeczywistych a i b.
VI sposób (szacowanie)
Nierówność a(a - 2b) + 2b2 > 0 jest równoważna nierówności
a2 + 2b2 > 2ab.
Dla dowolnych liczb rzeczywistych a, b prawdziwe są nierówności
a2 + 2b2 ≥ a2 + b2
oraz
a2 + b2 ≥ 2ab,
przy czym a2 + b2 = 2ab tylko wtedy, gdy a = b .
Ale z założenia a ≠ b, więc otrzymujemy
a2 + 2b2 ≥ a2 + b2 > 2ab.
To kończy dowód.
Zdający otrzymuje 1 p.
gdy
• zapisze nierówność w postaci (a – b)2 + b2 > 0
albo
• obliczy wyróżnik trójmianu kwadratowego w zależności od zmiennej a lub b, występującego po jednej stronie nierówności, gdy po drugiej stronie jest 0, i stwierdzi, że jest on niedodatni
albo
• obliczy wyróżnik trójmianu kwadratowego w zależności od zmiennej a lub b, występującego po jednej stronie nierówności, gdy po drugiej stronie jest 0 oraz rozważy jeden z przypadków Δ < 0 lub Δ = 0 i w tym przypadku doprowadzi rozumowanie do końca i na tym zakończy lub dalej popełni błędy.
Zdający otrzymuje 2 p.
gdy poda pełne uzasadnienie.
Uwaga
Jeżeli zdający sprawdza prawdziwość nierówności jedynie dla wybranych wartości
a i b, to otrzymuje 0 punktów za całe rozwiązanie.
Zasady oceniania III sposobu rozwiązania
Zdający otrzymuje 1 p.
gdy rozważy dwa przypadki:
w jednym, dla a ≠ 0, podzieli stronami nierówność przez a2, w drugim, dla b ≠ 0, podzieli stronami nierówność przez b2
i w jednym przypadku doprowadzi rozumowanie do końca.
Zdający otrzymuje 2 p.
gdy zapisze pełne rozumowanie.
Uwaga
Jeżeli zdający sprawdza prawdziwość nierówności jedynie dla wybranych wartości
a i b, to otrzymuje 0 punktów za całe rozwiązanie.
Zasady oceniania IV sposobu rozwiązania
Zdający otrzymuje 1 p.
gdy
• rozważy trzy przypadki i zapisze nierówności
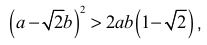
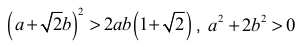
i na tym zakończy lub dalej popełni błędy.
albo
• przeprowadzi pełne rozumowanie w dwóch spośród trzech przypadków i na tym zakończy lub dalej popełni błędy.
Zdający otrzymuje 2p
gdy zapisze pełne rozumowanie.
Uwaga
Jeżeli zdający sprawdza prawdziwość nierówności jedynie dla wybranych wartości a i b, to otrzymuje 0 punktów za całe rozwiązanie.
Zasady oceniania V sposobu rozwiązania
Zdający otrzymuje 1 p.
gdy przeprowadzając dowód nie wprost, zapisze nierówność a (a - 2b) + 2b2 ≤ 0 w postaci (a - b)2 + b2 ≤ 0 i na tym zakończy lub dalej popełni błędy.
Zdający otrzymuje 2 p.
gdy zapisze pełne rozumowanie.
Uwaga
Jeżeli zdający sprawdza prawdziwość nierówności jedynie dla wybranych wartości a i b, to otrzymuje 0 punktów za całe rozwiązanie.
Zasady oceniania VI sposobu rozwiązania
Zdający otrzymuje 1 p.
gdy zapisze nierówność w postaci równoważnej a2 + 2b2 > 2ab oraz zapisze, że dla dowolnych liczb rzeczywistych a, b prawdziwe są nierówności:
a2 + 2b2 ≥ a2 + b2 oraz a2 + b2 ≥ 2ab
i na tym zakończy lub dalej popełni błędy
gdy zapisze pełne rozumowanie.
Uwaga
Jeżeli zdający sprawdza prawdziwość nierówności jedynie dla wybranych wartości a i b, to otrzymuje 0 punktów za całe rozwiązanie.