Odpowiedź:
Przykładowe rozwiązanie
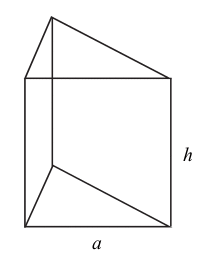
Przyjmijmy oznaczenia jak na rysunku:
a – krawędź podstawy,
h – wysokość graniastosłupa.
Objętość graniastosłupa prawidłowego trójkątnego o krawędzi podstawy a i wysokości h wyraża się wzorem:
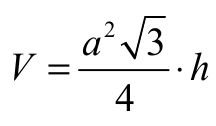
Stąd otrzymujemy:
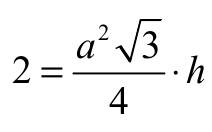
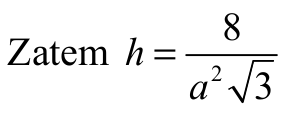
Pole powierzchni całkowitej graniastosłupa prawidłowego trójkątnego o krawędzi podstawy a i wysokości h jest równe:
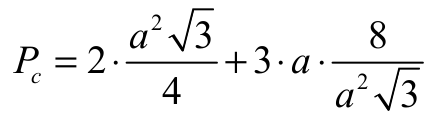
Stąd po podstawieniu h i przekształceniach otrzymujemy:
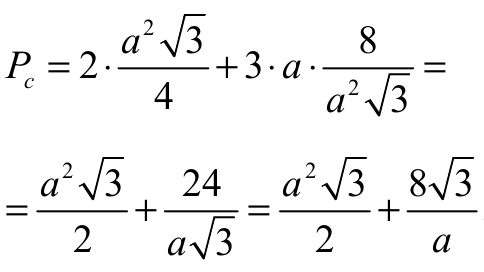
Z geometrycznych warunków zadania wynika, że a ∈ (0; + ∞ ).
Zapiszmy pole powierzchni całkowitej graniastosłupa prawidłowego trójkątnego jako funkcję ƒ
zmiennej a:
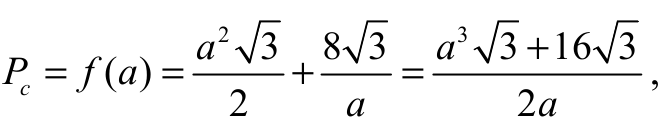
dla a ∈ (0; + ∞ ).
Wyznaczamy wartość najmniejszą funkcji ƒ w przedziale (0; + ∞ ).
W tym celu obliczmy pochodną funkcji ƒ:
W tym celu obliczmy pochodną funkcji ƒ:
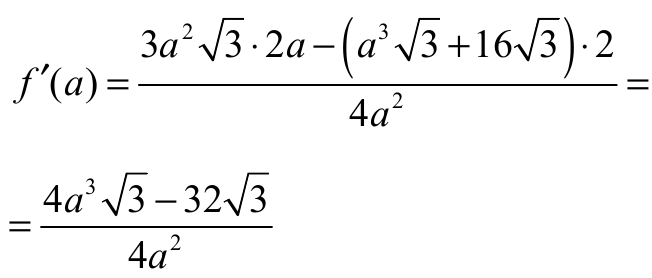
Szukamy miejsc zerowych pochodnej funkcji ƒ:
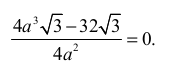
Ustalamy, że a = 2.
W przedziale (0; + ∞ ) pochodna funkcji ƒ ma tylko jedno miejsce zerowe a = 2.
W przedziale (0; + ∞ ) pochodna funkcji ƒ ma tylko jedno miejsce zerowe a = 2.
Ponadto
ƒ′(a) > 0 dla a ∈ (2; + ∞) oraz
ƒ′ (a) < 0 dla a ∈ (0; 2).
Wynika stąd, że dla a = 2 funkcja ƒ ma minimum lokalne, które jest jednocześnie najmniejszą
wartością funkcji ƒ w przedziale (0,+∞), ponieważ funkcja ƒ w przedziale ⟨2,+∞)
jest
rosnąca, a w przedziale (0,2⟩
funkcja ƒ jest malejąca.
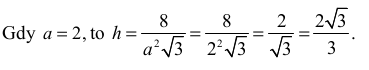
Natomiast pole powierzchni całkowitej graniastosłupa jest równe:
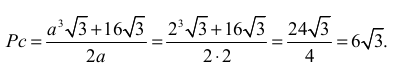
Odp.: Najmniejsze pole powierzchni całkowitej równe 6√3
ma graniastosłup prawidłowy trójkątny o wymiarach: krawędź podstawy a = 2 i wysokość
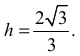
schemat punktacji
Rozwiązanie składa się z trzech etapów.
Pierwszy etap składa się z trzech części:
• oznaczenia krawędzi podstawy i wysokości graniastosłupa, np. odpowiednio przez a i h , oraz wyznaczenia wysokości graniastosłupa h w zależności od zmiennej a :
• oznaczenia krawędzi podstawy i wysokości graniastosłupa, np. odpowiednio przez a i h , oraz wyznaczenia wysokości graniastosłupa h w zależności od zmiennej a :
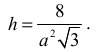
• zapisania pola powierzchni całkowitej graniastosłupa jako funkcji jednej zmiennej:
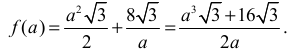
• wyznaczenia dziedziny funkcji ƒ: (0; +∞).
Za poprawne rozwiązanie tego etapu zdający otrzymuje 3 punkty .
I. 1. Za drugą część tego etapu zdający może otrzymać punkt w dwóch przypadkach:
– pierwszą część wykona bezbłędnie
albo
– błędnie wyznaczy h w zależności od a , ale otrzyma wartość h=k⋅a−2 , gdzie k jest liczbą
niewymierną.
I. 2. Punkt za część trzecią (wyznaczenie dziedziny funkcji) zdający otrzymuje niezależnie od
realizacji dwóch pierwszych części tego etapu, pod warunkiem, że rozważa wyznaczoną przez
siebie funkcję jednej zmiennej.
Drugi etap składa się z trzech części:
• wyznaczenia wzoru pochodnej funkcji ƒ:
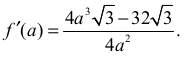
• obliczenia miejsca zerowego pochodnej funkcji ƒ: a = 2.
•
zbadania znaku pochodnej funkcji ƒ: ƒ′(a)>0 dla a ∈ (2; + ∞ ) ,
ƒ′(a)<0 dla a ∈ (0; 2) i uzasadnienia, że dla a = 2 funkcja ƒ osiąga
wartość najmniejszą.
Za poprawne rozwiązanie tego etapu zdający otrzymuje 3 punkty .
Uwagi do etapu II
II. 1. Jeżeli zdający wyznaczy pochodną funkcji z błędem, ale wyznaczona pochodna ma postać:
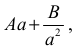
gdzie A , B są liczbami niewymiernymi, lub postać ułamka, w którego liczniku jest wielomian stopnia trzeciego, a w mianowniku ma2 , to zdający może otrzymać punkty za
część 2. i 3. tego etapu, o ile konsekwentnie obliczy miejsca zerowe pochodnej lub uzasadni
istnienie najmniejszej wartości rozważanej funkcji.
II. 2. Badanie znaku pochodnej zdający może opisać w inny sposób, np. szkicując wykres
funkcji, która w ten sam sposób jak pochodna zmienia znak.
II. 3. Za poprawne uzasadnienie, że rozważana funkcja posiada wartość najmniejszą dla
wyznaczonej wartości a , przy której pochodna się zeruje, można uznać sytuacje, gdy zdający:
– opisuje, słownie lub graficznie (np. przy użyciu strzałek), monotoniczność funkcji ƒ;
– zapisuje, że dla wyznaczonej wartości a funkcja f ma minimum lokalne i jest to jednocześnie
jej najmniejsza wartość. Jeżeli zdający nie przedstawi takiego uzasadnienia, to za II etap może
otrzymać co najwyżej 2 punkty .
II. 4. Jeżeli zdający błędnie wyznaczy dziedzinę funkcji, ale ta dziedzina jest podzbiorem
przedziału (0,+∞), to może otrzymać punkt za 3. część II etapu, gdy miejsce zerowe
pochodnej należy do wyznaczonej dziedziny.
Trzeci etap
Zapisanie, że krawędź podstawy i wysokość graniastosłupa prawidłowego trójkątnego o najmniejszym polu powierzchni całkowitej są równe odpowiednio
Zapisanie, że krawędź podstawy i wysokość graniastosłupa prawidłowego trójkątnego o najmniejszym polu powierzchni całkowitej są równe odpowiednio
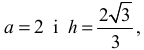
oraz obliczenie najmniejszego pola powierzchni całkowitej graniastosłupa 6√3
.
Za realizację tego etapu zdający otrzymuje 1 punkt .
Uwaga:
Jeżeli zdający pominie w rozważaniach jedną ze ścian graniastosłupa przy wyznaczaniu pola
powierzchni figury, to może otrzymać 5 punktów, o ile konsekwentnie rozwiąże zadanie do
końca bez innych błędów.