Odpowiedź:
Przykładowe rozwiązania
I sposób
Okrąg o równaniu x2 + y2 − 12x − 8y + 43 = 0 ma środek punkcie S1 = (6, 4) i promień r1 = 3 , a okrąg o równaniu x2 + y2 − 2ax + 4y + a2 − 77 = 0 ma środek w punkcie S2 = (a, − 2)
i promień r2 = 9 .
Ponieważ te okręgi mają dokładnie jeden punkt wspólny, więc odległość
pomiędzy środkami okręgów jest równa sumie promieni lub różnicy promieni:
|S1S2| = r1 + r2 lub |S1S2|= r2– r1
Otrzymujemy zatem równania
Zatem
Równanie (a − 6)2 = 108 ma dwa rozwiązania:
natomiast równanie (a − 6)2 = 0 ma jedno rozwiązanie a = 6 .
Zatem podane okręgi są styczne zewnętrznie dla
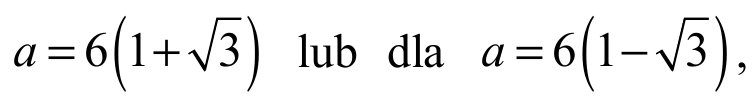
natomiast są okręgami stycznymi wewnętrznie dla a = 6 .
II sposób (wspólna styczna)
Okrąg o równaniu x2 + y2 − 12x − 8y + 43 = 0 ma środek punkcie S1 = (6, 4) i promień r1 = 3 , a okrąg o równaniu x2 + y2 − 2ax + 4y + a2 − 77 = 0 ma środek w punkcie S2 = (a, − 2) i promień r2 = 9 .
Okręgi te mają różne promienie, więc te okręgi mają dokładnie jeden punkt wspólny wtedy
i tylko wtedy, gdy mają dokładnie jedną wspólną styczną. Tak jest wtedy i tylko wtedy, gdy
odległość środka jednego z tych okręgów od tej stycznej jest równa promieniowi tego okręgu.
Jeśli tę wspólną styczną oznaczymy przez k , to wtedy mamy
odl (S1, k) = 3
Odejmując stronami równania okręgów otrzymujemy
(12 − 2a)x + 12y + a2 − 120 = 0 .
Jest to równanie wspólnej osi potęgowej tych okręgów. Jeśli teraz istnieją takie wartości
parametru a , dla których spełniony jest warunek odl (S1, k) = 3, to wtedy ta oś potęgowa jest
jednocześnie wspólną styczną tych okręgów. Otrzymujemy zatem równanie
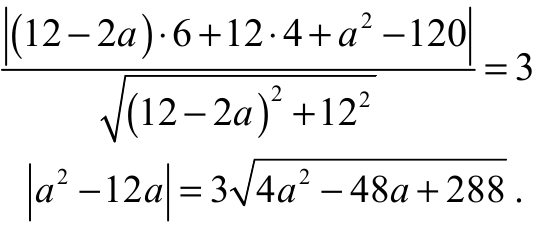
Obie strony tego równania są nieujemne, więc podnosząc je do kwadratu otrzymujemy równanie równoważne
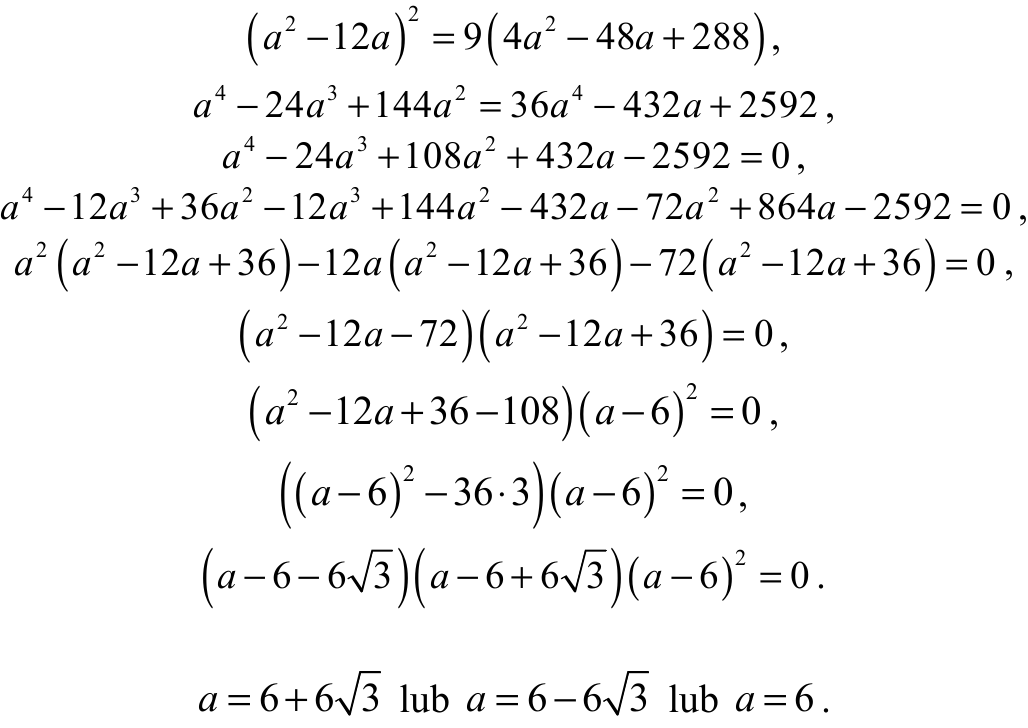
III sposób (równanie kwadratowe z parametrem)
Okrąg o równaniu x2 + y2 − 12x − 8y + 43 = 0 ma środek punkcie S1 = (6, 4) i promień r1 = 3 , a okrąg o równaniu x2 + y2 − 2ax + 4y + a2 − 77 = 0 ma środek w punkcie S2 = (a, − 2) i promień r2 = 9 .
Okręgi te mają różne promienie, więc te okręgi mają dokładnie jeden punkt wspólny wtedy i tylko wtedy, gdy układ równań
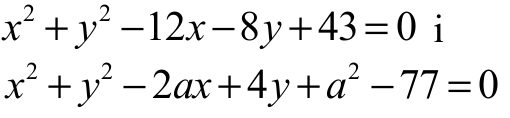
ma dokładnie jedno rozwiązanie. Stąd otrzymujemy kolejno
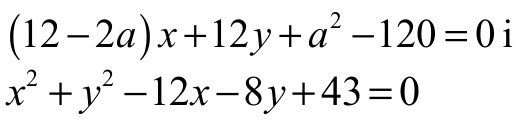
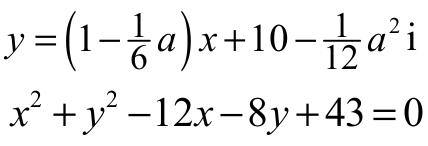
Stąd otrzymujemy równanie z niewiadomą x i parametrem a
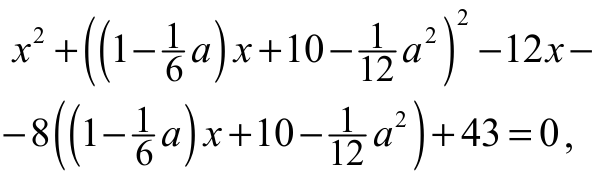
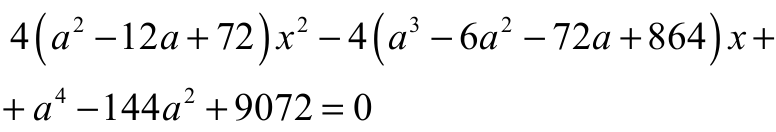
Ponieważ
dla każdego a , więc równanie jest kwadratowe.
Zatem układ równań ma dokładnie jedno rozwiązanie wtedy i tylko wtedy, gdy to równanie ma
dokładnie jedno rozwiązanie, a tak jest wtedy i tylko wtedy, gdy wyróżnik trójmianu
kwadratowego
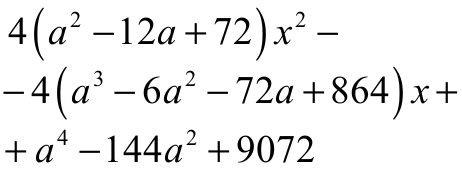
jest równy 0. Otrzymujemy więc równanie
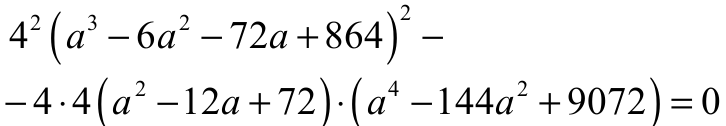
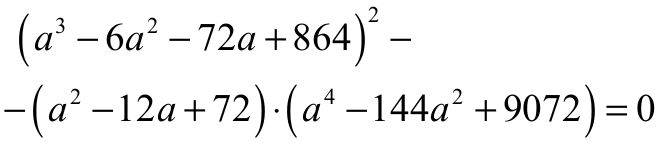
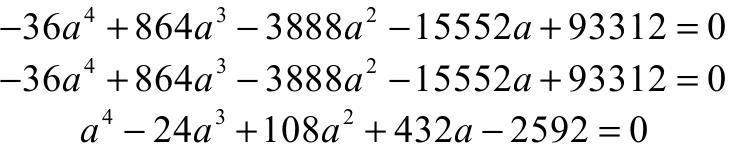
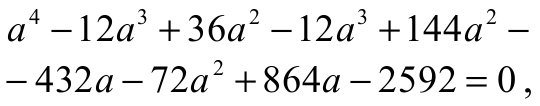
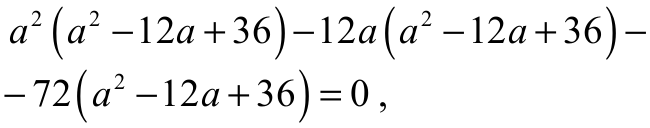
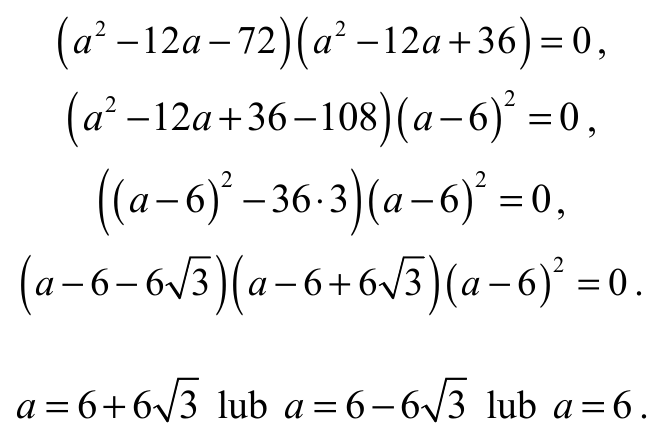
schemat punktacji
I. Rozwiązanie z wykorzystaniem odległości środków okręgów stycznych
Rozwiązanie składa się z trzech etapów:
Pierwszy etap polega na wyznaczeniu środków i promieni obu podanych okręgów oraz
ustaleniu warunków ogólnych ich położenia względem siebie.
Za poprawne rozwiązanie tego etapu zdający otrzymuje 2 punkty.
Drugi etap polega na wyznaczeniu równania z jedną niewiadomą, która opisuje warunek
styczności zewnętrznej i rozwiązanie tego równania.
Za poprawne rozwiązanie tego etapu zdający otrzymuje 2 punkty.
Trzeci etap polega na wyznaczeniu równania z jedną niewiadomą, która opisuje warunek
styczności wewnętrznej i rozwiązanie tego równania.
Za poprawne rozwiązanie tego etapu zdający otrzymuje 2 punkty.
Uwaga:
Etapy drugi i trzeci oceniane są niezależnie od siebie.
Etapy drugi i trzeci oceniane są niezależnie od siebie.
Podział punktów za pierwszy etap rozwiązania:
Zdający otrzymuje 2 punkty, gdy:
zapisze współrzędne środków i promienie obu okręgów:
S1 = (6,4) , r1 = 3 oraz S2 = (a,−2) , r2 = 9
oraz
zapisze warunki styczności obu okręgów w dwóch przypadkach:
|S1S2|= r1 + r2 , |S1S2|= r2 – r1.
Zdający otrzymuje 2 punkty, gdy:
zapisze współrzędne środków i promienie obu okręgów:
S1 = (6,4) , r1 = 3 oraz S2 = (a,−2) , r2 = 9
oraz
zapisze warunki styczności obu okręgów w dwóch przypadkach:
|S1S2|= r1 + r2 , |S1S2|= r2 – r1.
Zdający otrzymuje 1 punkt, gdy:
• zauważy i zapisze, że są dwa przypadki styczności okręgów, tj. styczność zewnętrzną i wewnętrzną
• zauważy i zapisze, że są dwa przypadki styczności okręgów, tj. styczność zewnętrzną i wewnętrzną
albo
• wyznaczy współrzędne środków okręgów i obliczy promienie obu okręgów.
• wyznaczy współrzędne środków okręgów i obliczy promienie obu okręgów.
Podział punktów za drugi etap rozwiązania:
Zdający otrzymuje 2 punkty, gdy zapisze równanie:
Zdający otrzymuje 2 punkty, gdy zapisze równanie:
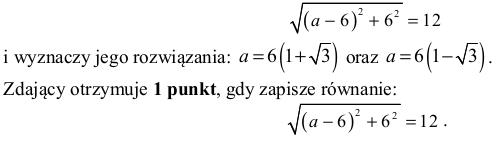
Podział punktów za trzeci etap rozwiązania:
Zdający otrzymuje 2 punkty, gdy zapisze równanie:
Zdający otrzymuje 2 punkty, gdy zapisze równanie:
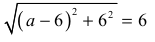
i wyznaczy jego rozwiązanie: a = 6 .
Zdający otrzymuje 1 punkt, gdy zapisze równanie:
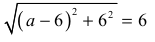
Uwagi
1. Jeżeli zdający prowadzi poprawne rozumowanie na każdym etapie rozwiązania zadania
i rozwiązuje zadanie do końca, ale popełnia jedynie błędy rachunkowe, to może
otrzymać co najwyżej 5 punktów, o ile popełnione błędy nie ułatwiają rozważanego
zagadnienia na żadnym etapie rozwiązania.
2. Jeżeli zdający prowadzi poprawne rozumowanie na każdym etapie rozwiązania zadania,
rozwiązuje zadanie do końca i jedynym błędem, który jednak nie ułatwia rozwiązania zadania na żadnym etapie rozwiązania, jest błąd, polegający na:
a) niepoprawnym wyznaczeniu promieni okręgów lub współrzędnych ich środków, to zdający otrzymuje co najwyżej 4 punkty;
b) zastosowaniu niepoprawnej metody wyznaczania odległości środków okręgów, to zdający otrzymuje co najwyżej 4 punkty;
b) zastosowaniu niepoprawnej metody wyznaczania odległości środków okręgów, to zdający otrzymuje co najwyżej 4 punkty;
c) zastosowaniu niepoprawnego wzoru
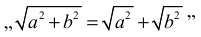
lub

to zdający otrzymuje co najwyżej 4 punkty.
3. Jeżeli zdający sporządzi poprawną ilustrację graficzną i na tej podstawie zapisze, że
dla a = 6 podane okręgi są styczne wewnętrznie i na tym zakończy, to otrzymuje
2 punkty.
4. Jeżeli zdający rozważa tylko jeden przypadek styczności okręgów i w tym przypadku
rozwiąże zadanie do końca, popełniając jeden błąd opisany w uwadze 2., to otrzymuje
co najwyżej 2 punkty.
II. Rozwiązanie z wykorzystaniem wspólnej stycznej lub równania kwadratowego z parametrem
Zdający otrzymuje 6 punktów , gdy wyznaczy wszystkie wartości parametru a: a = 6 lub a = 6 + 6√3 lub a = 6 − 6√3.
Zdający otrzymuje 5 punktów , gdy wyznaczy tylko jedno z rozwiązań równania z jedną niewiadomą a zapisze równanie kwadratowe z niewiadomą a , np.: a = 6 .
Zdający otrzymuje 4 punkty , gdy zapisze równanie wielomianowe z niewiadomą a :
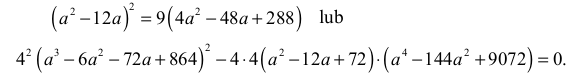
Zdający otrzymuje 3 punkty , gdy
• zapisze równanie z niewiadomą a:
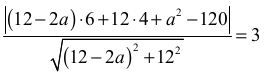
albo
• zapisze równanie kwadratowe z jedną niewiadomą x (lub y ) i parametrem a oraz zapisze, że równanie to musi mieć jedno rozwiązanie, np.:
• zapisze równanie kwadratowe z jedną niewiadomą x (lub y ) i parametrem a oraz zapisze, że równanie to musi mieć jedno rozwiązanie, np.:
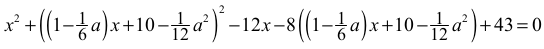
oraz Δ=0.
Zdający otrzymuje 2 punkty , gdy
• zapisze równanie prostej (12−2a)x+12y+a2−120=0 oraz zapisze współrzędne
środka i promień jednego z okręgów oraz zapisze, że okręgi mają dokładnie jeden punkt
wspólny, gdy odległość środka jednego okręgu od wspólnej stycznej tych okręgów jest
równa promieniowi tego okręgu
albo
• zapisze równanie z jedną niewiadomą x (lub y ) i parametrem a , np.:
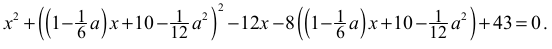
Zdający otrzymuje 1 punkt , gdy
• zapisze równanie prostej (12−2a)x+12y+a2−120=0
• zapisze równanie prostej (12−2a)x+12y+a2−120=0
albo
• zapisze współrzędne środka i promień jednego z okręgów oraz zapisze, że okręgi mają
dokładnie jeden punkt wspólny, gdy odległość środka jednego okręgu od wspólnej
stycznej tych okręgów jest równa promieniowi tego okręgu.
Uwaga:
Jeżeli zdający zapisze równanie prostej, będącej osią potęgową okręgów i traktuje to równanie
jak równanie kwadratowe zmiennej a , a następnie wyznacza konkretne wartości x , y , a ,
sprawdza dla wyznaczonych wartości prawdziwość równania osi potęgowej okręgów i podaje
jedno z rozwiązań zadania, to otrzymuje 3 punkty .