Odpowiedź:
Przykładowe rozwiązania
I sposób
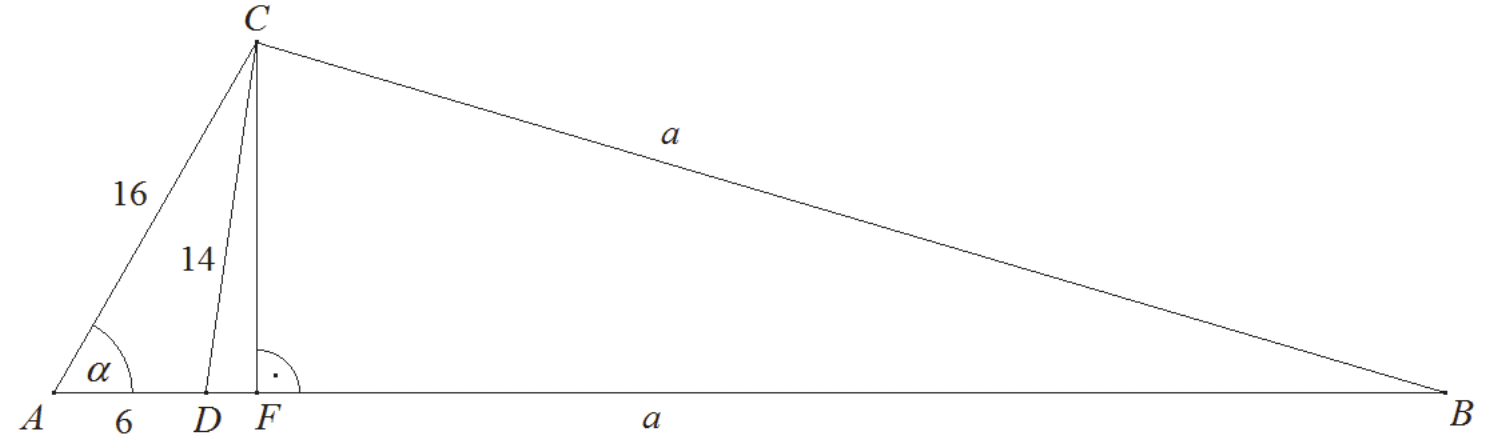
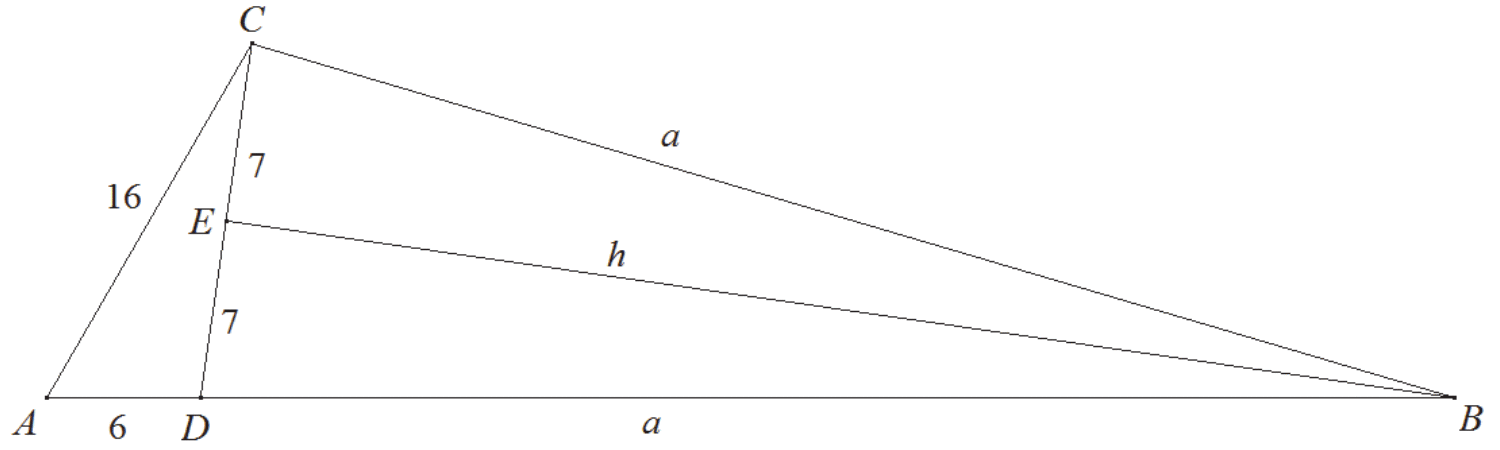
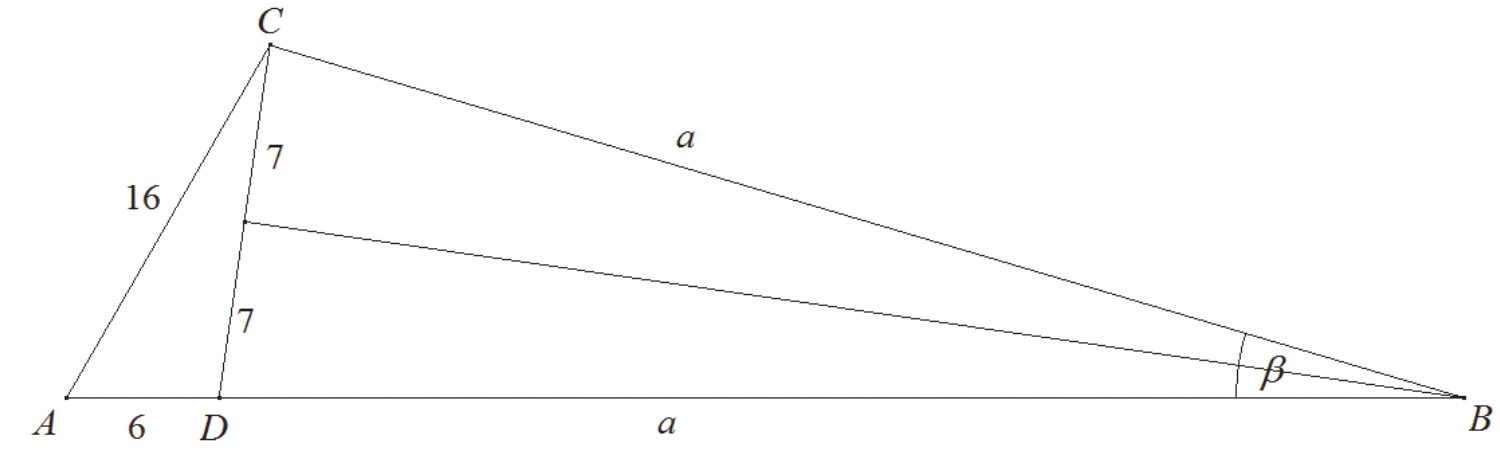
Przyjmijmy oznaczenia jak na rysunku.
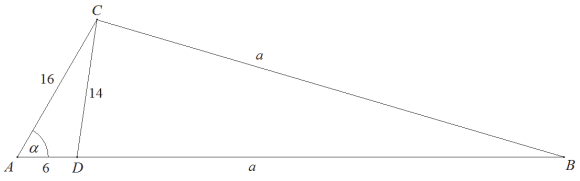
Z twierdzenia cosinusów dla trójkąta ADC otrzymujemy
142 = 162 + 62 − 2 ⋅ 16 ⋅ 6 ⋅ cos α .
142 = 162 + 62 − 2 ⋅ 16 ⋅ 6 ⋅ cos α .
Stąd
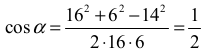
Zatem α = 60° .
Z twierdzenia cosinusów dla trójkąta ABC otrzymujemy
a2 = 162 + (a + 6)2 − 2 ⋅ 16 ⋅ (a + 6) ⋅ cos α ,
Z twierdzenia cosinusów dla trójkąta ABC otrzymujemy
a2 = 162 + (a + 6)2 − 2 ⋅ 16 ⋅ (a + 6) ⋅ cos α ,
a2 = 256 + a2 + 12a + 36 − 2 ⋅ 16 ⋅ (a + 6) ⋅ ½
4 a = 196 ,a = 49
Obwód trójkąta ABC jest równy
LABC = 16 + 6 + 2 ⋅ 49 = 120 .
LABC = 16 + 6 + 2 ⋅ 49 = 120 .
II sposób
Przyjmijmy oznaczenia jak na rysunku.
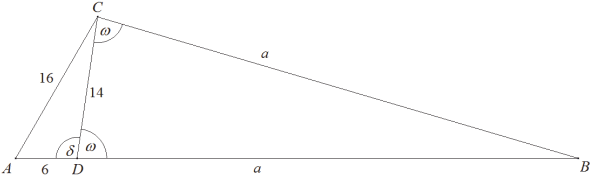
Z twierdzenia cosinusów dla trójkąta ADC otrzymujemy
162 = 142 + 62 − 2 ⋅ 14 ⋅ 6 ⋅ cos δ .
Stąd
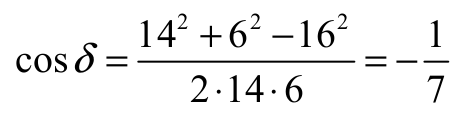
Zatem
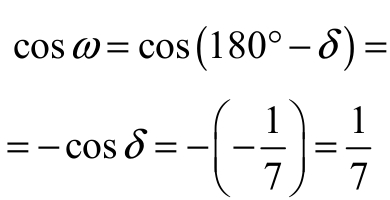
Z twierdzenia cosinusów dla trójkąta BCD otrzymujemy
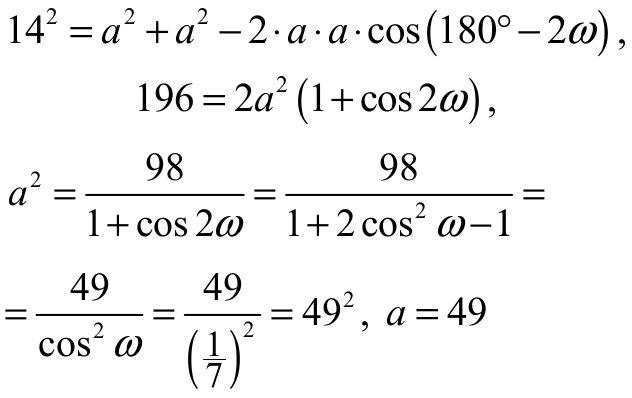
albo
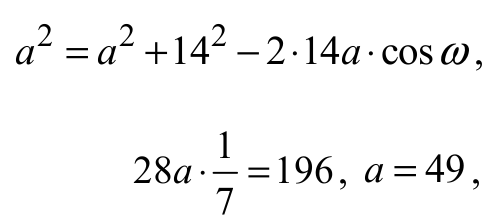
albo z twierdzenia sinusów otrzymujemy
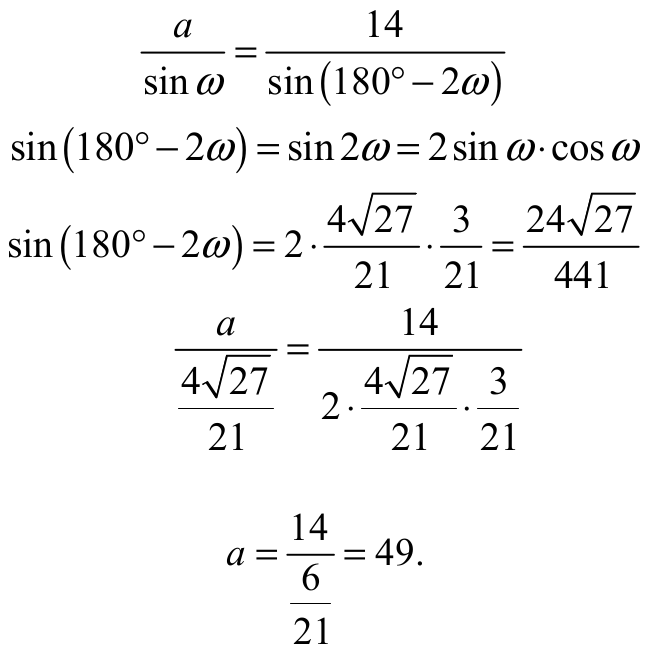
Więc obwód trójkąta ABC jest równy
LABC = 16 + 6 + 2 ⋅ 49 = 120 .
LABC = 16 + 6 + 2 ⋅ 49 = 120 .
III sposób
Przyjmijmy oznaczenia jak na rysunku.
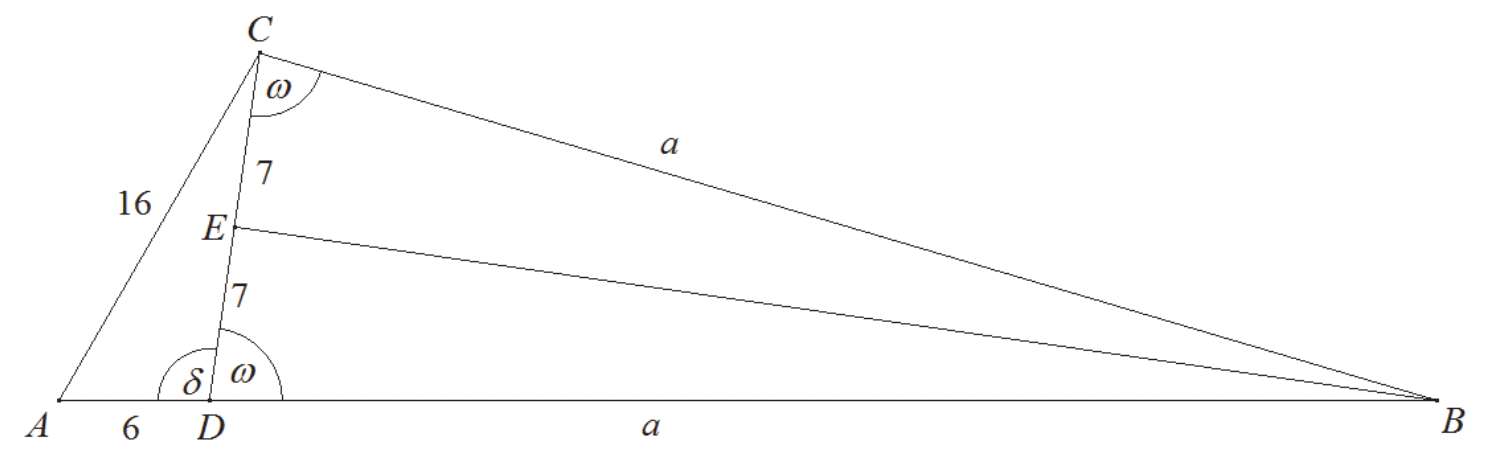
Z twierdzenia cosinusów dla trójkąta ADC otrzymujemy
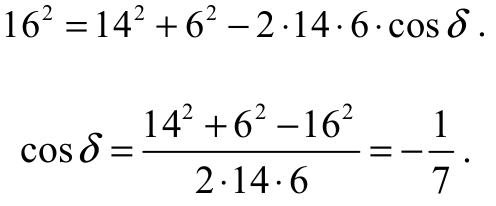
Zatem
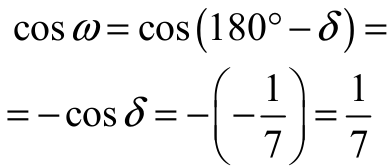
Trójkąt BCD jest równoramienny, więc spodek E wysokości BE tego trójkąta jest środkiem boku CD. Zatem
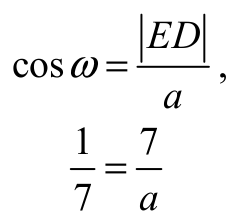
Stąd a = 49 , więc obwód trójkąta ABC jest równy
LABC = 16 + 6 + 2 ⋅ 49 = 120
IV sposób
Poprowadźmy wysokość CF trójkąta ABC i przyjmijmy oznaczenia jak na rysunku.
Z twierdzenia cosinusów dla trójkąta ADC otrzymujemy
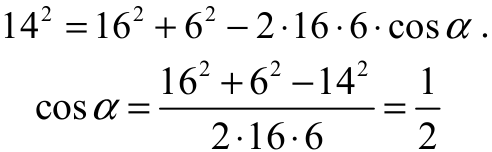
Zatem α = 60° . Trójkąt AFC jest więc połową trójkąta równobocznego o boku długości 16.
Stąd |AF| = 8 i |CF| = 8√3 .
Stąd |AF| = 8 i |CF| = 8√3 .
W rezultacie
|DF| = |AF| − |AD| = 8 − 6 = 2
oraz
|BF| = |BD| − |DF| = a − 2
Z twierdzenia Pitagorasa dla trójkąta BCF otrzymujemy
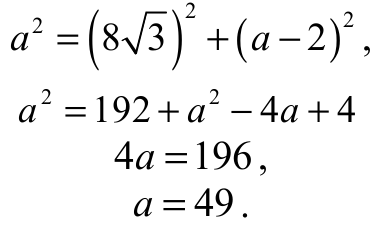
Obwód trójkąta ABC jest równy
LABC = 16 + 6 + 2 ⋅ 49 = 120
V sposób
Poprowadźmy wysokość CF trójkąta ABC i przyjmijmy oznaczenia jak na rysunku.
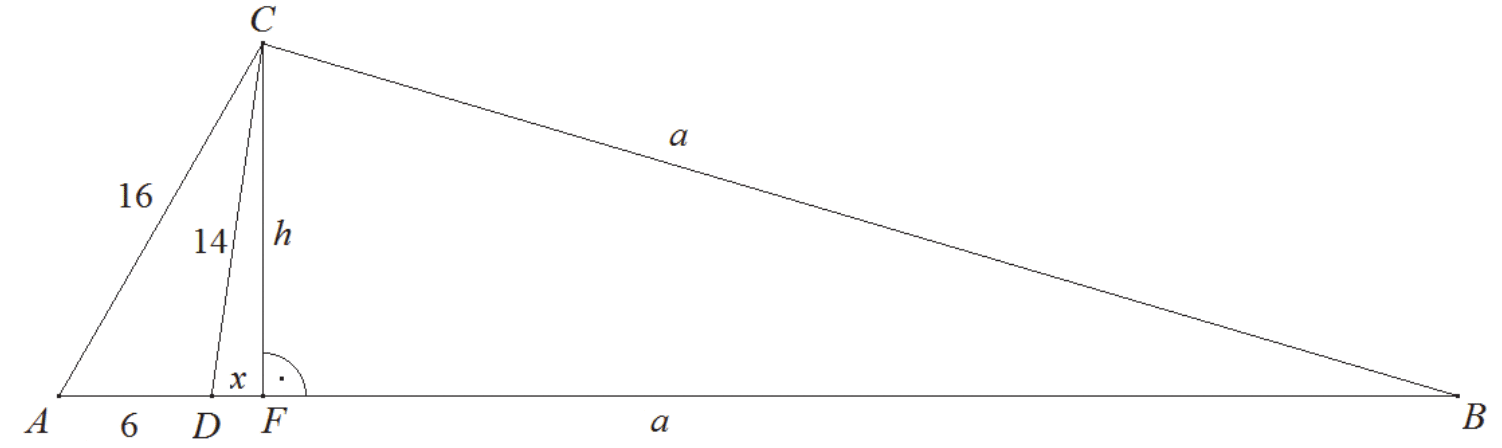
Z twierdzenia Pitagorasa dla trójkątów AFC i DFC otrzymujemy
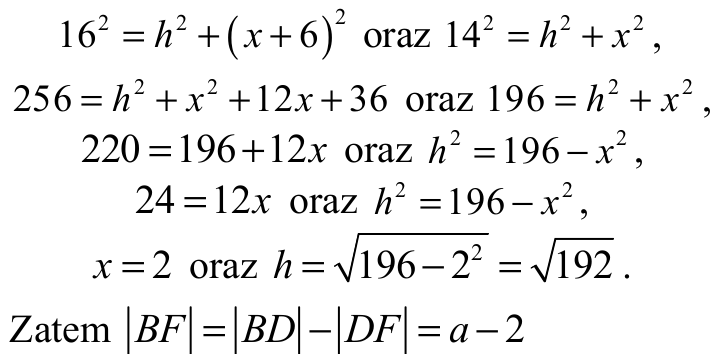
Z twierdzenia Pitagorasa dla trójkąta BCF otrzymujemy
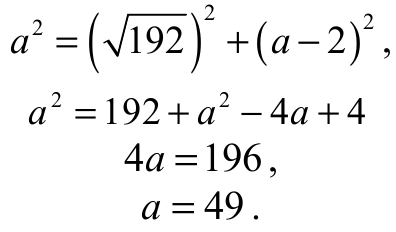
Obwód trójkąta ABC jest równy
LABC = 16 + 6 + 2 ⋅ 49 = 120 .
VI sposób
Przyjmijmy oznaczenia jak na rysunku.
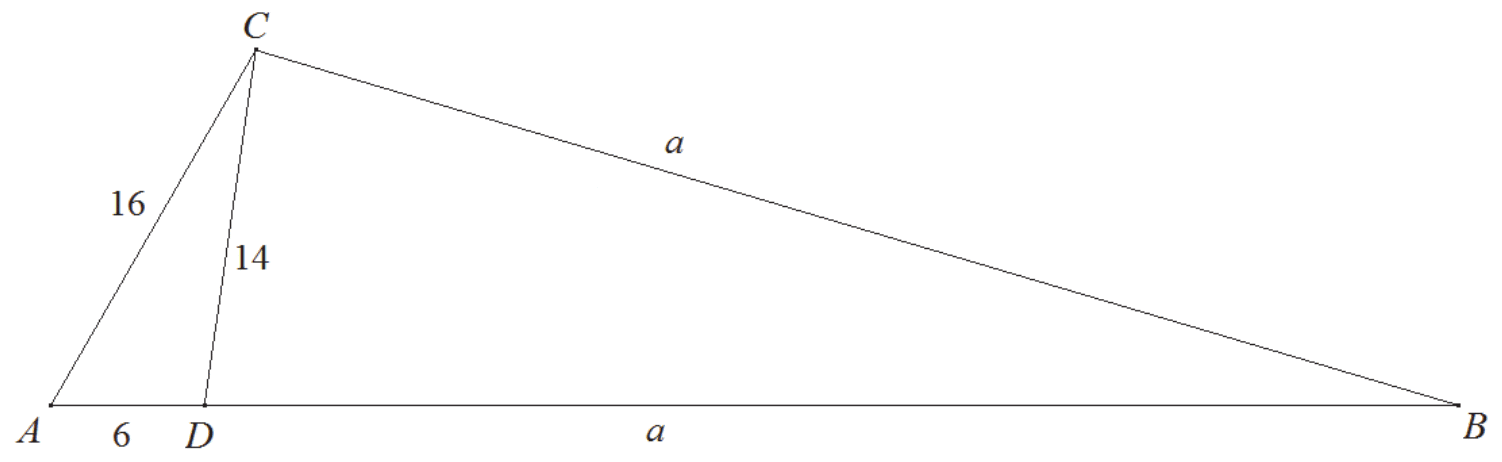
Z twierdzenia Stewarta dla trójkąta ABC otrzymujemy
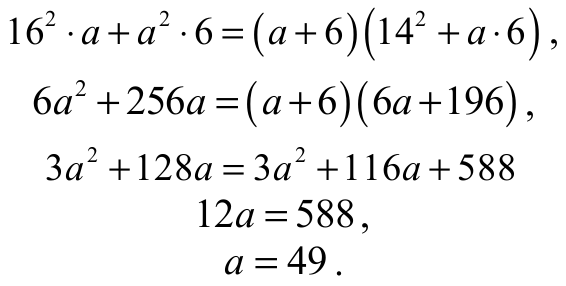
Obwód trójkąta ABC jest równy
LABC = 16 + 6 + 2 ⋅ 49 = 120 .
VII sposób
Przyjmijmy oznaczenia jak na rysunku.
Obliczmy pole trójkąta ADC ze wzoru Herona.
Połowa obwodu tego trójkąta jest równa
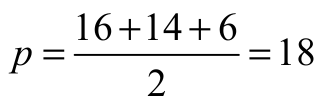
więc
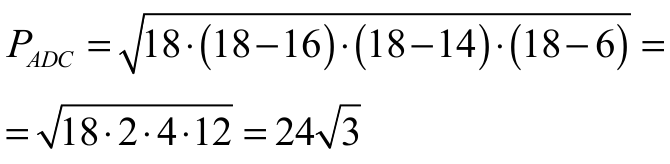
Zatem
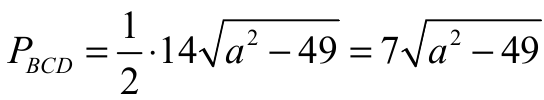
Ponieważ trójkąty ADC i BCD mają wspólną wysokość opuszczoną z wierzchołka C, więc
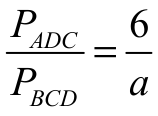
czyli
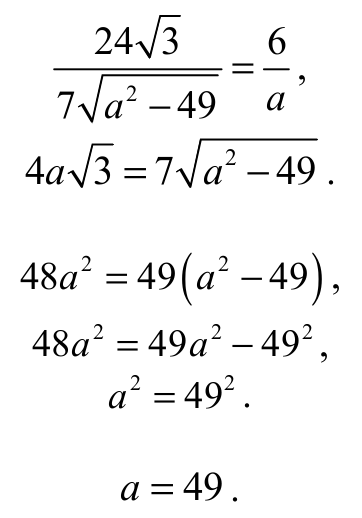
Obwód trójkąta ABC jest równy
LABC = 16 + 6 + 2 ⋅ 49 = 120 .
VIII sposób
Przyjmijmy oznaczenia jak na rysunku.
Obliczmy pole trójkąta ADC ze wzoru Herona.
Połowa obwodu tego trójkąta jest równa
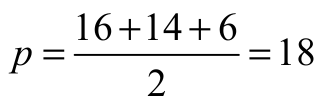
więc
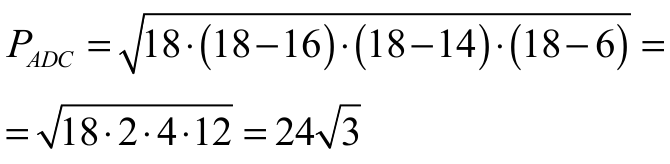
Pola trójkątów ABC i BCD są równe odpowiednio
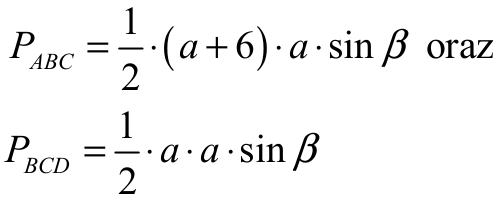
Ponieważ, PABC = PBDC + PADC , więc
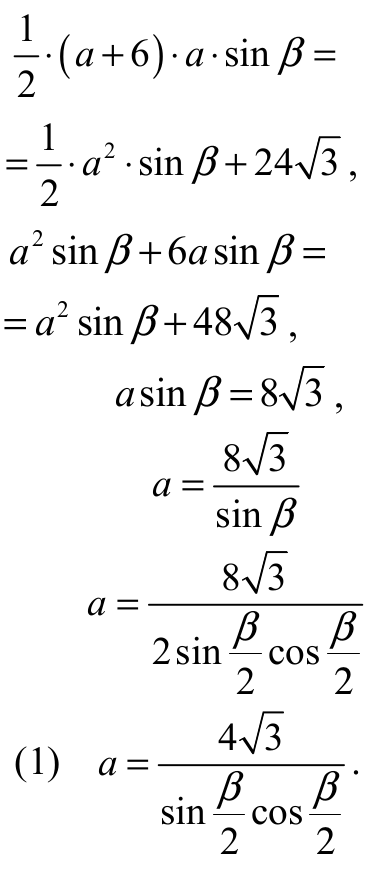
Ponieważ trójkąt BCD jest równoramienny, więc wysokość opuszczona na podstawę CD dzieli ten trójkąt na dwa przystające trójkąty prostokątne. Zatem
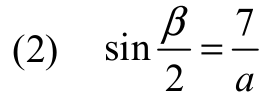
Z jedynki trygonometrycznej otrzymujemy
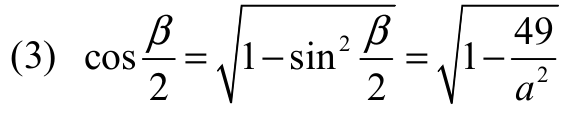
Z (1), (2) i (3) otrzymujemy równanie z niewiadomą a
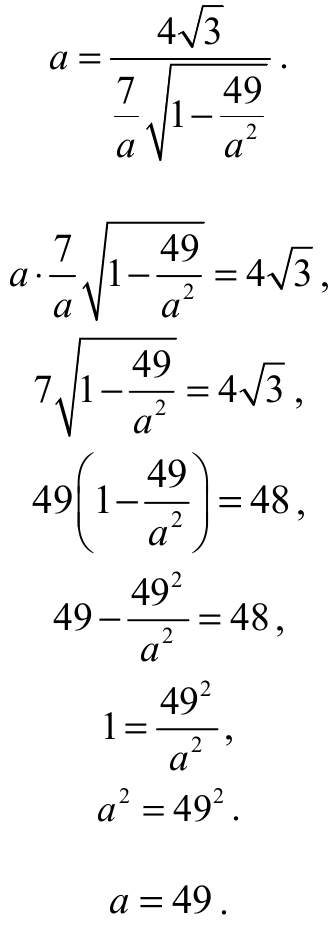
Obwód trójkąta ABC jest równy
LABC = 16 + 6 + 2 ⋅ 49 = 120 .
IX sposób
Poprowadźmy wysokości CF i BE trójkąta BCD i przyjmijmy oznaczenia jak na rysunku.
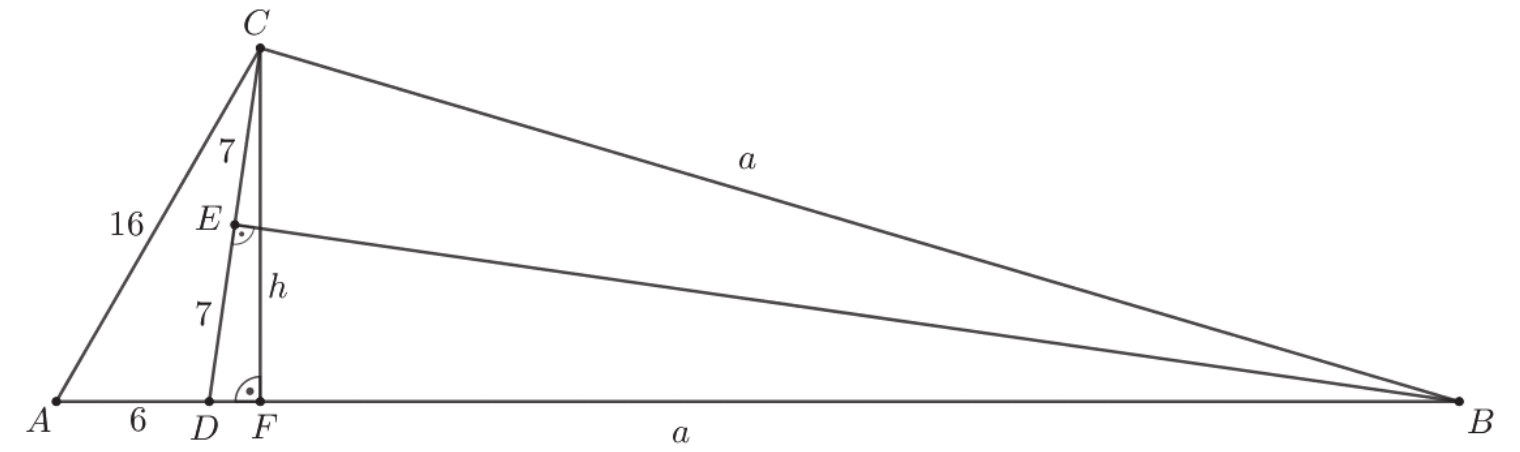
Obliczmy pole trójkąta ADC ze wzoru Herona.
Połowa obwodu tego trójkąta jest równa
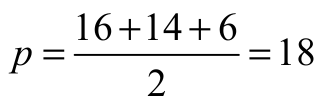
więc
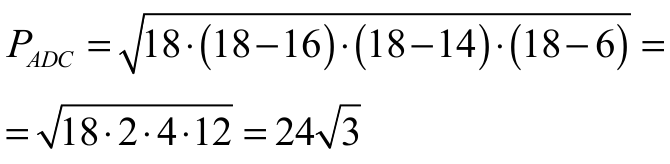
Odcinek CF jest też wysokością trójkąta ADC , więc pole tego trójkąta jest równe
Otrzymujemy zatem
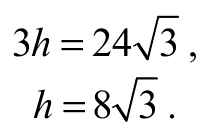
Z twierdzenia Pitagorasa dla trójkąta CDF otrzymujemy
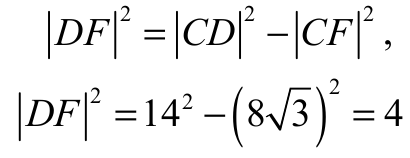
Stąd |DF| = 2
Trójkąt BCD jest równoramienny, więc spodek E wysokości BE tego trójkąta jest środkiem podstawy CD . Zatem

Obwód trójkąta ABC jest równy
LABC = 16 + 6 + 2 ⋅ 49 = 120 .
X sposób
Przyjmijmy oznaczenia jak na rysunku.
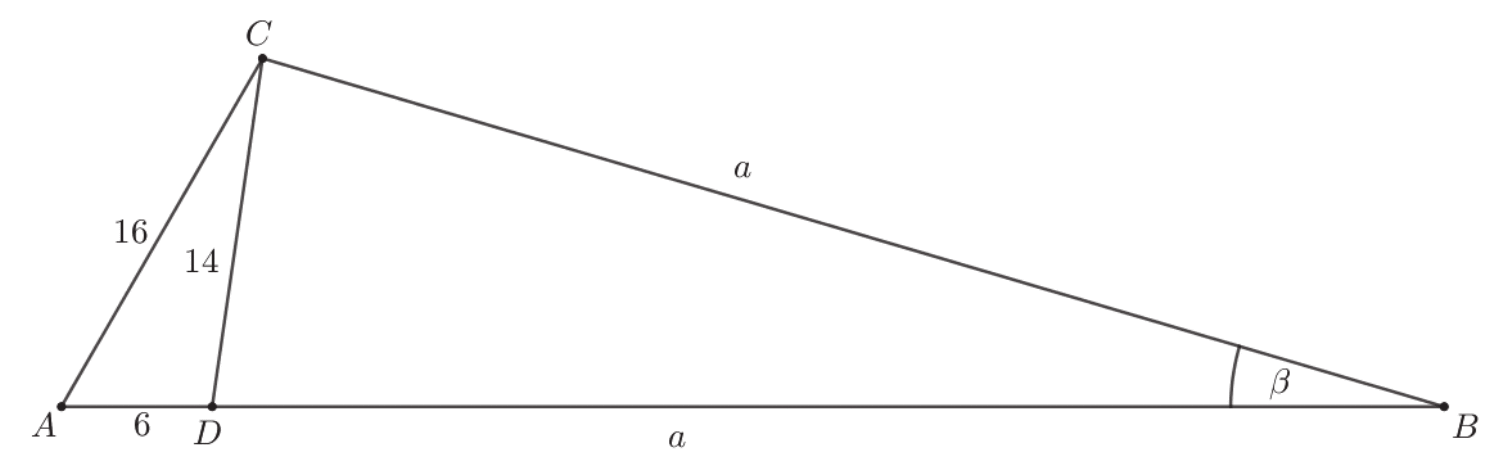
Z twierdzenia cosinusów dla trójkąta BCD otrzymujemy
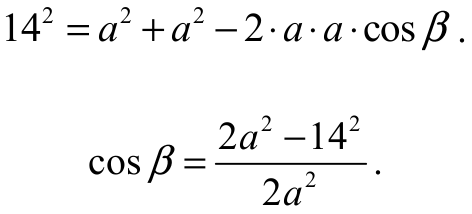
Z twierdzenia cosinusów dla trójkąta ABC otrzymujemy
Stąd i z poprzednio otrzymanego równania otrzymujemy równanie z jedną niewiadomą a
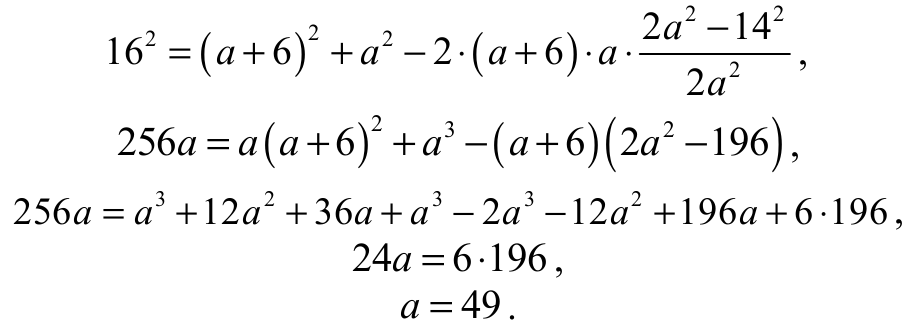
Obwód trójkąta ABC jest równy
LABC = 16 + 6 + 2 ⋅ 49 = 120 .
XI sposób
Poprowadźmy wysokość CF trójkąta BCD i przyjmijmy oznaczenia jak na rysunku.
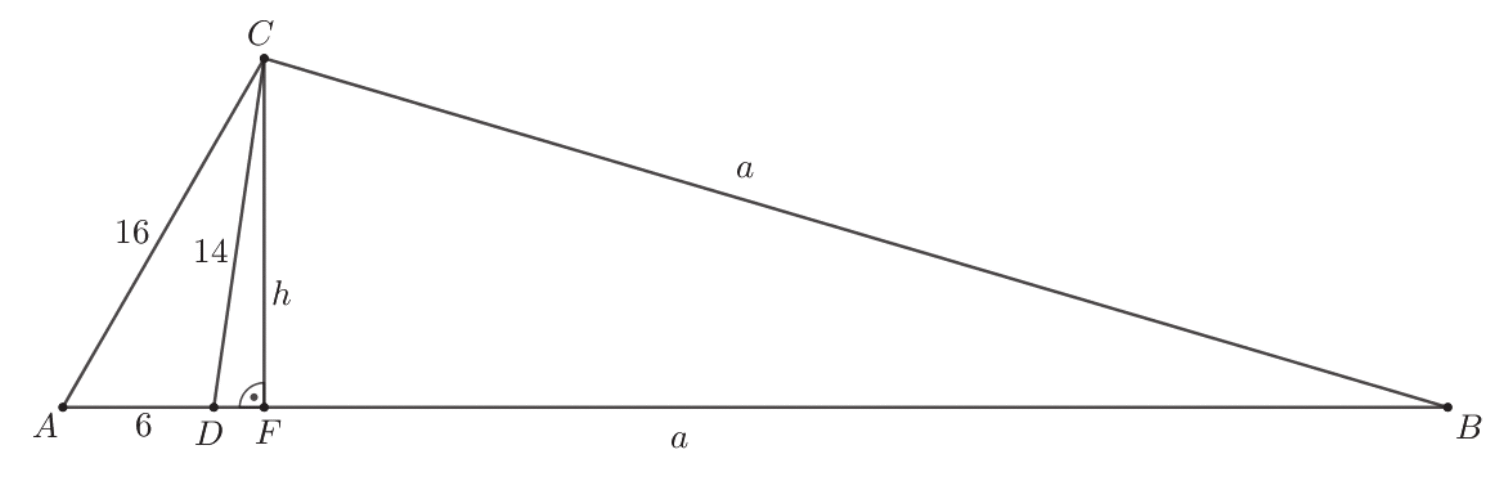
Obliczmy pole trójkąta ADC ze wzoru Herona.
Połowa obwodu tego trójkąta jest równa
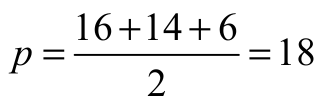
więc
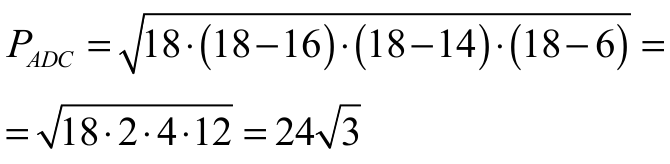
Odcinek CF jest też wysokością trójkąta ADC , więc pole tego trójkąta jest równe
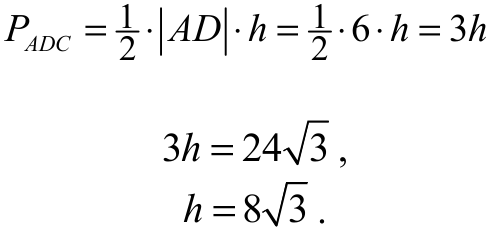
Pole trójkąta BCD jest więc równe
Zapiszmy pole trójkąta ABC , stosując wzór Herona. Połowa obwodu trójkąta ABC jest równa
więc
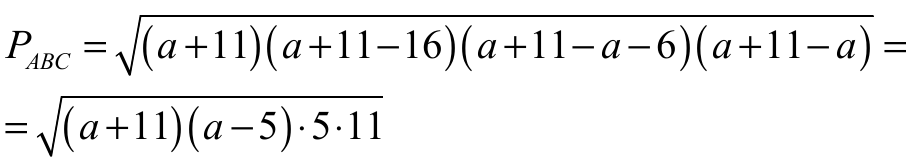
Obie strony tego równania są dodatnie, więc podnosząc je do kwadratu otrzymujemy równanie równoważne
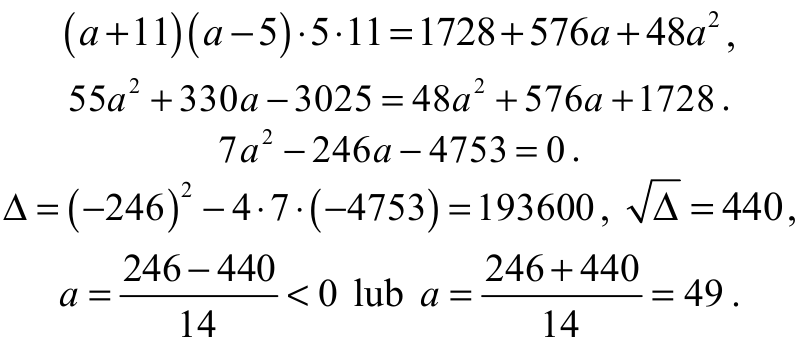
Obwód trójkąta ABC jest równy
LABC = 16 + 6 + 2 ⋅ 49 = 120 .
schemat punktacji
Rozwiązanie pełne 4 p.
Zdający obliczy obwód trójkąta ABC: LABC = 120 .
Pokonanie zasadniczych trudności zadania 3 p.
Zdający zapisze równanie wymierne z jedną niewiadomą a, np.:
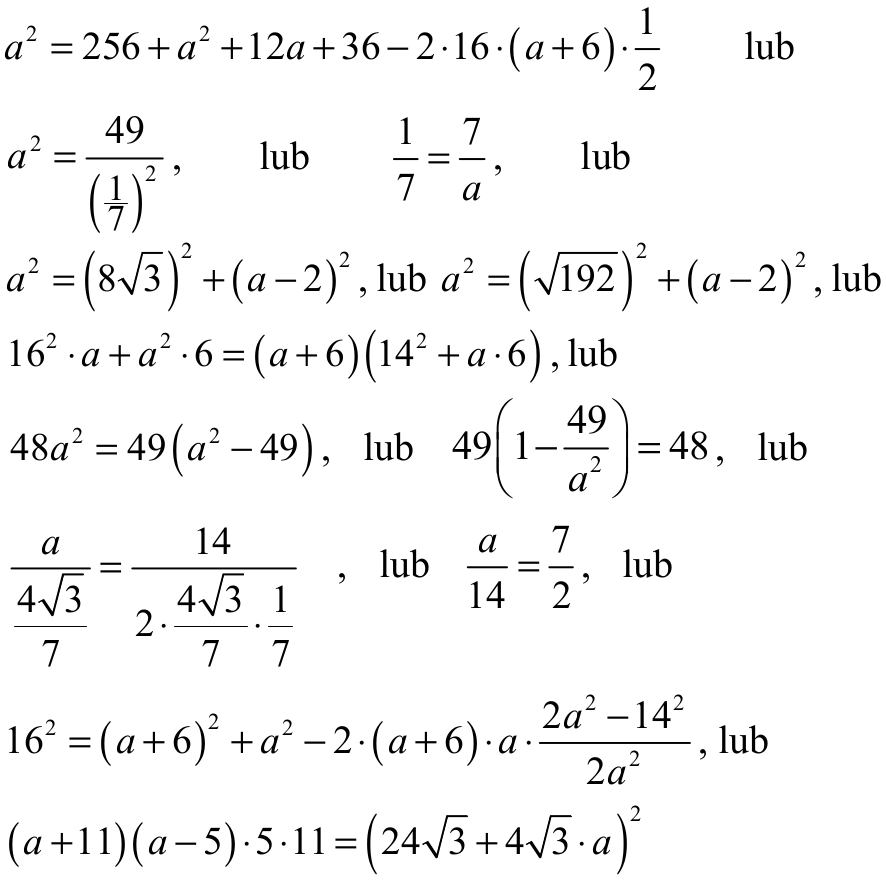
Rozwiązanie, w którym jest istotny postęp 2 p.
Zdający
• obliczy cosα = ½ oraz zapisze równanie wynikające z twierdzenia cosinusów dla trójkąta ABC:
albo
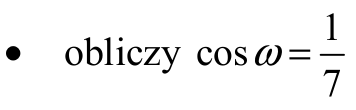
oraz zapisze równanie wynikające z twierdzenia cosinusów dla trójkąta BCD, np.:
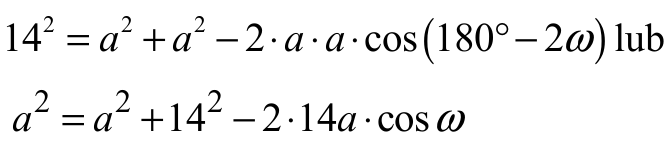
albo
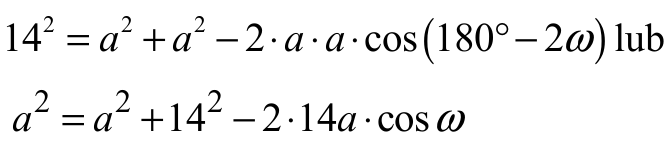
albo
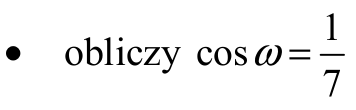
oraz zapisze równanie wynikające z definicji cosinusa w trójkącie
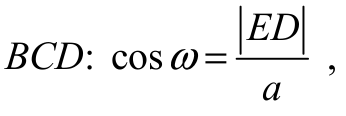
albo
• obliczy |AF| = 8 , |CF| = 8√3 oraz wyznaczy długość odcinka BF w zależności od a:
|BF| = a − 2 ,
albo
• obliczy pole trójkąta ADC , wyznaczy pole trójkąta BCD w zależności od a oraz wyznaczy stosunek pól trójkątów ADC i BCD w zależności od a: PADC = 24√3,
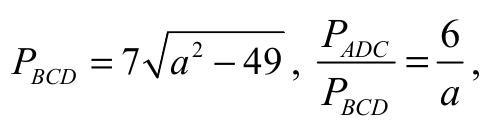
albo
• obliczy pole trójkąta ADC, wysokość CF oraz długość odcinka DF: PADC = 24√3, |CF| = 8√3, |DF| = 2 ,
albo
• zapisze układ równań z dwiema niewiadomymi a i cos β :
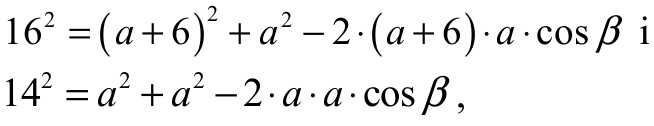
albo
• obliczy pole trójkąta ADC oraz wyznaczy pola trójkątów ABC i BCD w zależności od a:
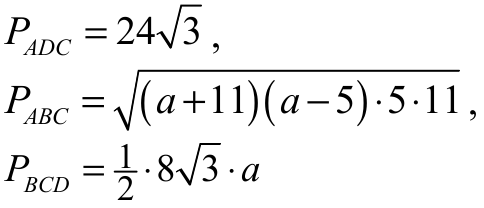
i na tym zakończy lub dalej popełnia błędy.
Rozwiązanie, w którym postęp jest niewielki, ale konieczny na drodze do pełnego rozwiązania zadania 1 p.
Zdający
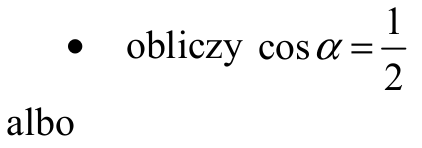
• zapisze równanie wynikające z twierdzenia cosinusów dla trójkąta ABC:
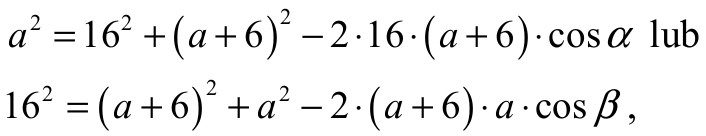
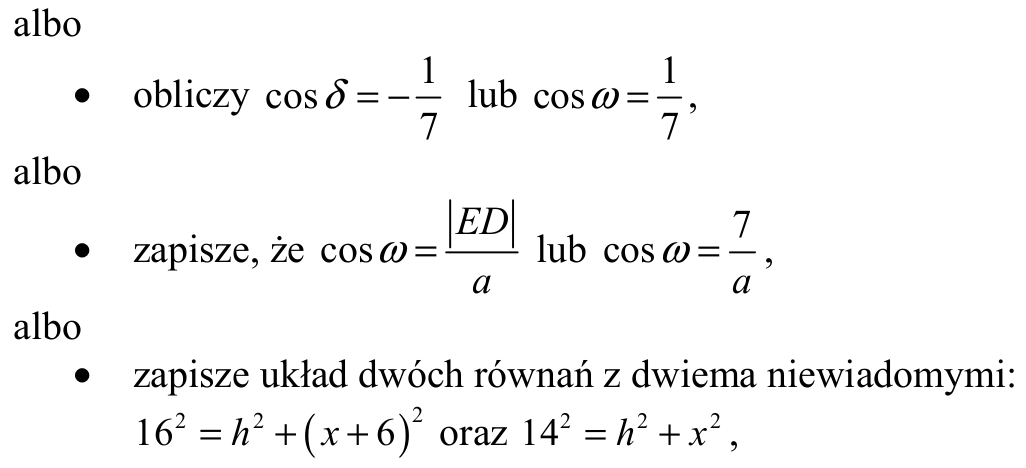
albo
• obliczy pole trójkąta ADC i wyznaczy pole trójkąta BCD w zależności od a – długości boku BC:
albo
• obliczy pole trójkąta ADC i wyznaczy pola trójkątów ABC i BCD w zależności od a – długości boku BC oraz sin β :
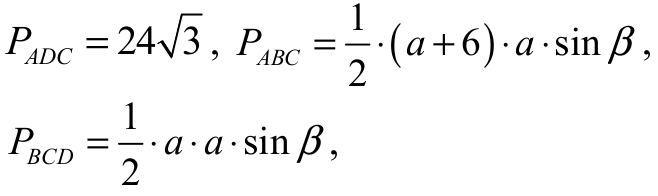
albo
• obliczy pole trójkąta ADC oraz wysokość CF:
albo
• zapisze równanie wynikające z twierdzenia cosinusów dla trójkąta BCD:
i na tym zakończy lub dalej popełnia błędy.
Uwagi:
1. Jeżeli zdający realizuje strategię rozwiązania i popełnia jedynie błędy rachunkowe, to może otrzymać 3 punkty, o ile popełnione błędy nie ułatwiają rozważanego zagadnienia na żadnym etapie rozwiązania.
2. Jeżeli zdający pominie współczynnik ½ we wzorze na pole trójkąta, to może otrzymać 3 punkty za rozwiązanie zadania konsekwentnie do końca.
3. Jeżeli zdający realizuje strategię rozwiązania i jedynym błędem, który jednak nie ułatwia rozważania zagadnienia na żadnym etapie rozwiązania, jest błąd, polegający na niepoprawnym zastosowaniu:
a) twierdzenia cosinusów lub twierdzenia sinusów, lub niewłaściwym podstawieniu do wzoru z tego twierdzenia,
b) definicji funkcji trygonometrycznej,
c) wzoru Herona,
d) twierdzenia Pitagorasa,
e) wzoru redukcyjnego,
f) wzoru na pole trójkąta z sinusem kąta między bokami,
g) twierdzenia Stewarta,
b) definicji funkcji trygonometrycznej,
c) wzoru Herona,
d) twierdzenia Pitagorasa,
e) wzoru redukcyjnego,
f) wzoru na pole trójkąta z sinusem kąta między bokami,
g) twierdzenia Stewarta,
h) wzoru
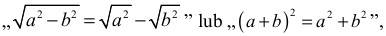
to zdający otrzymuje co najwyżej 2 punkty za rozwiązanie całego zadania.
4. Jeżeli zdający realizuje strategię rozwiązania, i popełnia jeden błąd, wymieniony w uwadze 3., a ponadto popełnia błędy rachunkowe, to otrzymuje 1 punkt.
5. Jeżeli zdający stosuje przybliżenia funkcji trygonometrycznych i tym samym zmienia aspekt rozważanego zagadnienia, to może otrzymać co najwyżej 3 punkty za całe rozwiązanie.
6. Jeżeli zdający zakłada, że kąt CAD ma miarę 60 stopni, to może uzyskać jedynie punkty za te części rozwiązania, w których nie korzysta z tego nieuprawnionego założenia.