Odpowiedź:
Przykładowe rozwiązania
I sposób („przystawanie trójkątów – I”)
Niech P będzie środkiem podstawy AB tego trójkąta. Poprowadźmy przez punkty M i N
proste równoległe do podstawy AB trójkąta, a ich punkty przecięcia z prostą CP oznaczmy
odpowiednio K i L. Oznaczmy też x = |AM| = |CN| , y = |MC| , p = |AS| , q = |MK| , jak na
rysunku.
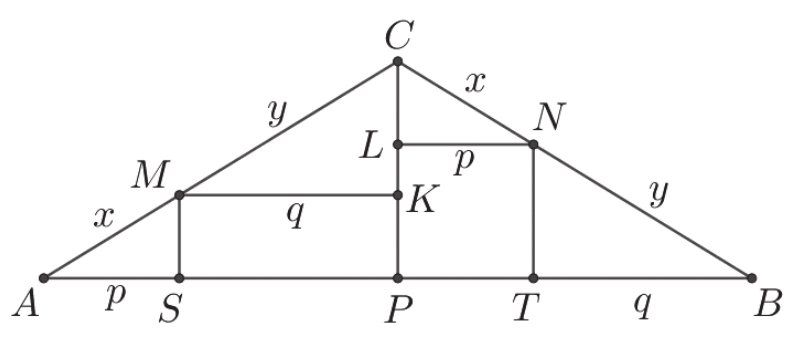
Ponieważ trójkąt ABC jest równoramienny, więc |NB| = |MC| = y . Trójkąty ASM i NLC są przystające, gdyż oba są prostokątne, |AM| = |CN| oraz |∢BAC| = |∢ABC| = |∢LNC| oraz |∢AMS| = 90 ° − |∢BAC| = 90 ° − |∢LNC| = |∢NCL| . Podobnie uzasadniamy, że trójkąty MKC i BTN są przystające.
Zatem
|PT| = |LN| = |AS| = p
oraz
|SP| = |MK| = |TB| = q
Stąd wynika, że
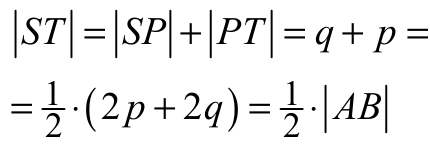
II sposób („przystawanie trójkątów – II”)
Niech P będzie środkiem podstawy AB tego trójkąta. Poprowadźmy przez punkt N prostą
równoległą do podstawy AB trójkąta, a punkt jej przecięcia z prostą CP oznaczmy przez L.
Oznaczmy też x = |AM| = |CN| , p = |AS| , jak na rysunku.
Trójkąty ASM i NLC są przystające, gdyż oba są prostokątne, |AM| = |CN| ,
|∢BAC| = |∢ABC| = |∢LNC|
oraz
|∢AMS| = 90 ° − |∢BAC| = 90 ° − |∢LNC| = |∢NCL|
Stąd wynika, że
|PT| = |LN| = |AS| = p
Ponieważ trójkąt ABC jest równoramienny, więc
|AP| = |BP|
Stąd wynika, że
|ST| = |SP| + |PT| = (|AP| − p) + p = |AP| = ½ ⋅ |AB|
Uwaga:
Analogiczne rozumowanie możemy przeprowadzić, wychodząc od pary trójkątów przystających MKC i BTN (oznaczenia jak w I sposobie oceniania).
Analogiczne rozumowanie możemy przeprowadzić, wychodząc od pary trójkątów przystających MKC i BTN (oznaczenia jak w I sposobie oceniania).
III sposób („podobieństwo trójkątów”)
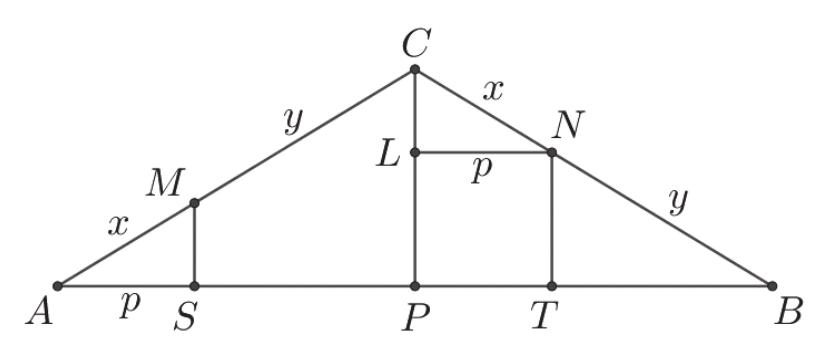
Niech P będzie środkiem podstawy AB tego trójkąta. Oznaczmy też x = |AM| = |CN| , b = |AC| = |BC| , a = |AP| , jak na rysunku.
Ponieważ P jest spodkiem wysokości trójkąta równoramiennego, więc |BP| = |AP| = a .
Trójkąty ASM i APC są podobne na mocy cechy kkk, ponieważ obydwa są trójkątami
prostokątnymi (odcinki SM i PC są równoległe), a kąt PAC jest kątem wspólnym obu
trójkątów. Stąd wynika, że
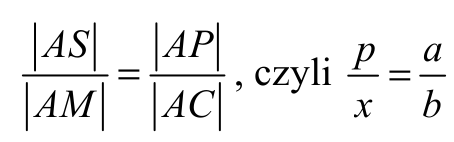
Stąd
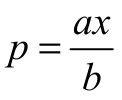
Zatem
Ponieważ NT || CP i kąt CBP jest kątem wspólnym, więc na mocy cechy kkk trójkąt BTN jest podobny do trójkąta BPC . Stąd wynika, że
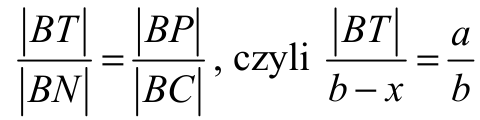
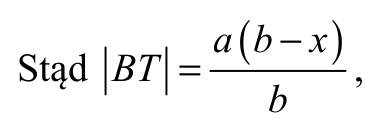
więc
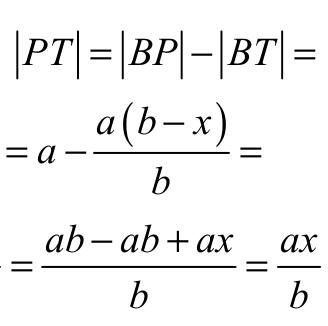
Zatem
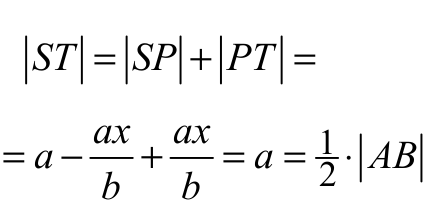
To kończy dowód.
IV sposób („twierdzenia Talesa”)
Niech P będzie środkiem podstawy AB tego trójkąta. Oznaczmy też
x = |AM| = |CN| ,
b = |AC| = |BC| ,
a = |AP| ,
p = |AS| ,
q = |PT| ,
jak na rysunku.
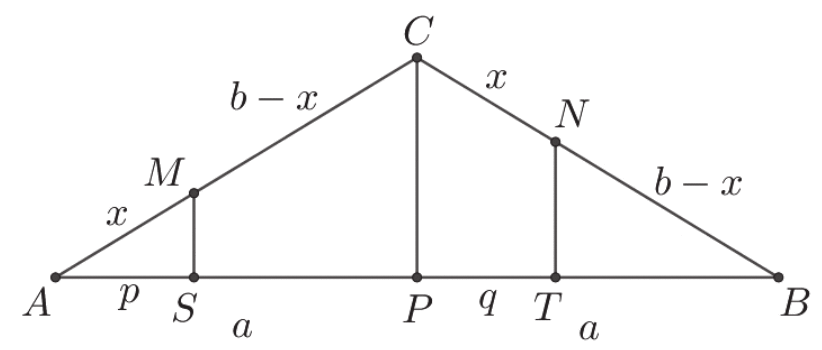
Ponieważ trójkąt ABC jest równoramienny, a P jest spodkiem jego wysokości, więc
|BN| = |MC| = b − x i |BP| = |AP| = a
Z twierdzenia Talesa otrzymujemy
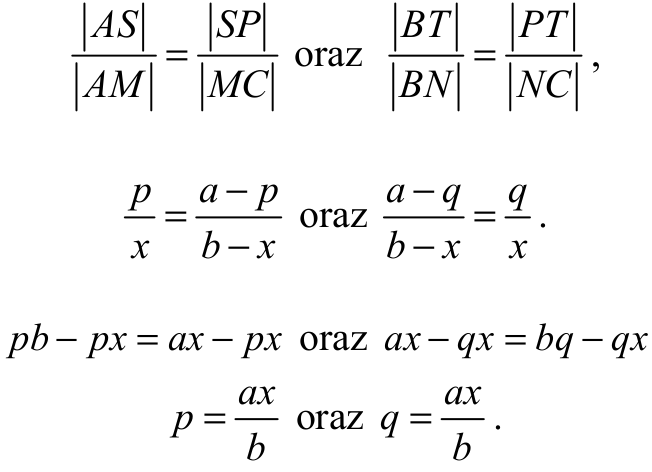
Zatem
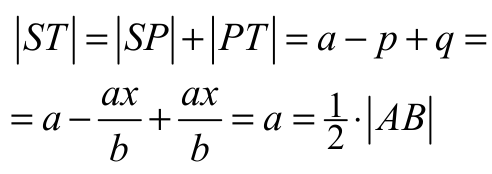
To kończy dowód.
V sposób („trygonometria”)
Oznaczmy
α = |∢BAC| = |∢ABC| ,
x = |AM| = |CN| ,
y = |MC| ,
2a = |AP| ,
jak na rysunku.
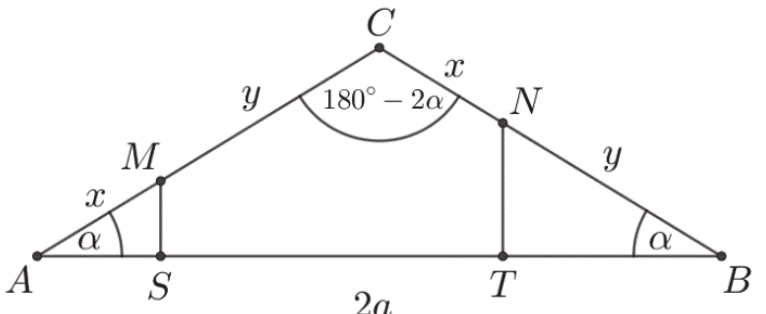
Wtedy |NB| = |BC| − x = |AC| − x = y
oraz |∢ACB| = 180 ° − 2α
Z twierdzenia cosinusów dla trójkąta ABC otrzymujemy
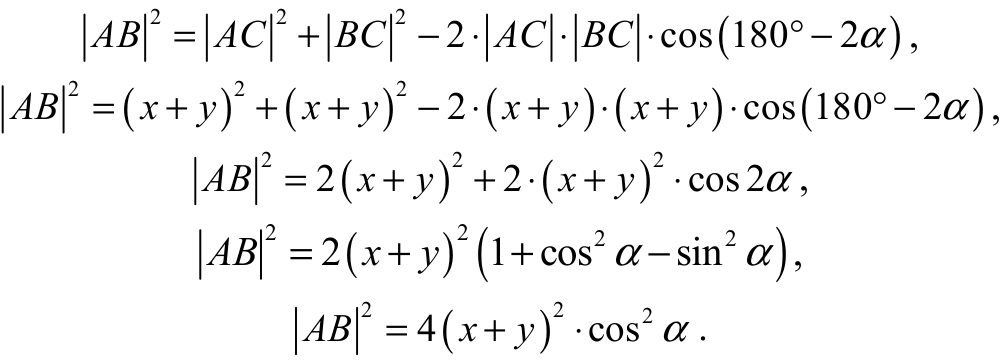
Z trójkątów ASM i BTN otrzymujemy
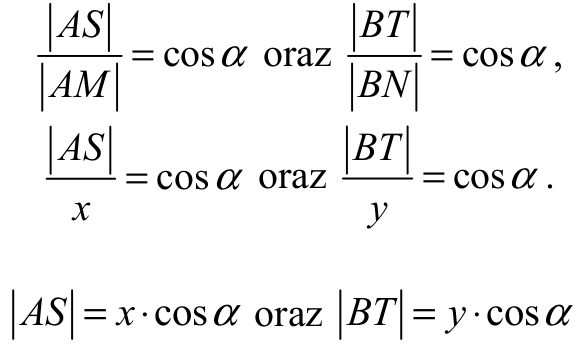
Zatem
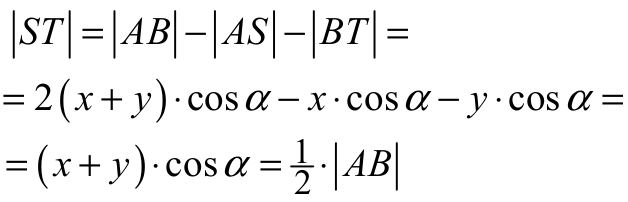
To kończy dowód.
VI sposób („trójkąty równoramienne”)
Narysujmy odcinek MZ równoległy do prostej BC taki, że koniec Z tego odcinka leży na podstawie AB trójkąta ABC oraz odcinek NZ. Oznaczmy też
x = |AM| = |CN| ,
y = |MC| ,
p = |AS| ,
q = |TB| ,
jak na rysunku.
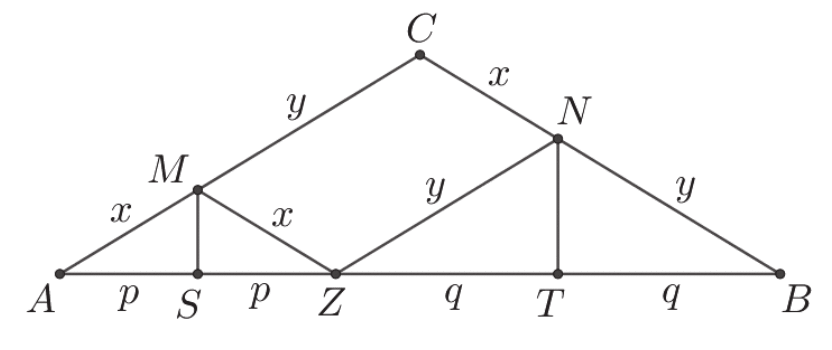
Wtedy kąty odpowiadające AZM i ABC są równe. To oznacza, że trójkąt AZM jest równoramienny. Stąd wynika, że
|MZ| = |AM| = |CN| = x .
Zatem czworokąt MZNC jest równoległobokiem (jego boki MZ i CN są równoległe i mają równe długości), co oznacza, że
|ZN| = |MC| = y .
To z kolei oznacza, że trójkąt ZBN jest równoramienny. Punkty S i T to spodki wysokości trójkątów równoramiennych, więc
|AS| = |SZ| = p
oraz
|ZT| = |TB| = q
Stąd
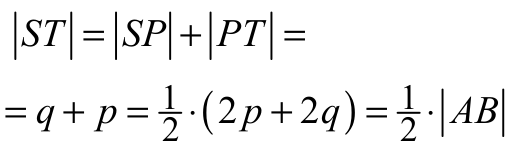
To kończy dowód.
schemat punktacji
Rozwiązanie pełne 3 p.
Zdający zapisze pełne, poprawne rozumowanie.
Zdający zapisze pełne, poprawne rozumowanie.
Pokonanie zasadniczych trudności zadania 2 p.
Zdający
• zapisze, że trójkąty ASM i NLC lub trójkąty MKC i BTN są przystające, nie uzasadni tego przystawania i uzasadni tezę
albo
•
zapisze dwie proporcje wynikające z podobieństwa trójkątów pozwalające
(wraz z równością |AP| = |BP| ) wyznaczyć zależność między długościami
odcinków ST i AB, np.:
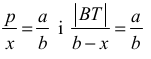
albo
•
zapisze dwie proporcje wynikające z twierdzenia Talesa pozwalające
(wraz z równością |AP| = |BP| ) wyznaczyć zależność między długościami
odcinków ST i AB, np.:
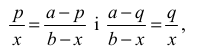
albo
• zapisze długości odcinków AB, AS i BT w zależności od długości odcinków x = |AM| ,
y = |MC| oraz kąta α w postaci: |AB| = 2(x+y)⋅cosα , |AS| = x⋅cosα ,
|BT| = y⋅cosα ,
albo
• narysuje odcinek MZ równoległy do BC oraz odcinek ZN lub odcinek NZ równoległy do
AC oraz odcinek MZ, zapisze, że trójkąty AMZ i ZBN są równoramienne, ale nie uzasadni,
że czworokąt MZNC jest równoległobokiem i poprawnie uzasadni tezę
i na tym zakończy lub dalej popełni błędy.
Rozwiązanie,
w którym postęp jest wprawdzie niewielki, ale konieczny na drodze do
całkowitego rozwiązania zadania 1 p.
Zdający
• zapisze, że trójkąty ASM i NLC są przystające lub trójkąty MKC i BTN są przystające
albo
• zapisze, że trójkąty, np. ASM i APC są podobne lub zapisze proporcję wynikającą z tego
podobieństwa,
albo
• zapisze proporcję wynikającą z twierdzenia Talesa, np.:
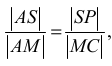
albo
• wyznaczy długość odcinka AB w zależności od długości odcinków x = |AM| , y = |MC| oraz kąta α : |AB|2 = (x+ y)2 + (x+ y)2 − 2⋅(x+y)⋅(x+y)⋅cos(180°−2α) ,
albo
• zapisze dwie zależności:
• zapisze dwie zależności:
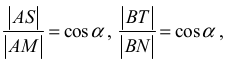
albo
• narysuje odcinek MZ równoległy do BC oraz odcinek ZN lub odcinek NZ równoległy
do AC oraz odcinek MZ
i na tym zakończy lub dalej popełni błędy.
Uwagi
1. Za uzasadnienie przystawania trójkątów prostokątnych np.: ASM i NLC uznajemy
a) powołanie się na cechę przystawania kbk, o ile na rysunku nie występują sprzeczne
oznaczenia kątów,
b) zaznaczenie na rysunku jednej pary odpowiednich kątów ostrych w tych trójkątach.
2. W III i IV sposobie rozwiązania nie wymagamy uzasadnienia podobieństwa trójkątów lub
powołania się na twierdzenie Talesa.
3. Jeżeli zdający rozpatrzy tylko szczególny przypadek, w którym punkty M i N, są środkami
boków AC i BC, to otrzymuje 0 punktów za całe rozwiązanie.
4. Jeżeli zdający zakłada, że trójkąt ABC jest równoboczny i korzysta z tego założenia, to za
całe rozwiązanie otrzymuje 0 punktów.
5. Jeżeli zdający przedstawia rozwiązanie, w którym odwołuje się tylko do argumentów
pozamatematycznych, np. „przesuwa” punkty M i N po odcinkach AC i BC z tymi samymi
szybkościami, to może otrzymać 1 punkt za zauważenie, że rzuty prostokątne na prostą AB
odcinków równych, z których jeden leży na prostej AC, a drugi na prostej BC są równe.