Odpowiedź:
Przykładowe rozwiązania
I sposób
Nierówność możemy przekształcić w sposób równoważny
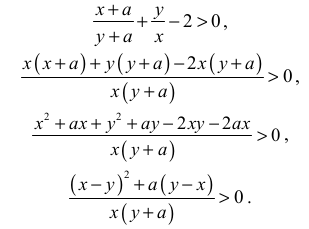
Z założenia y > 0 , x > 0 i a > 0 . Zatem y + a > 0 i x > 0 , co oznacza, że mianownik ułamka
stojącego po lewej strony otrzymanej nierówności jest dodatni. Kwadrat
(x − y)2
jest
nieujemny, a z założenia x < y wynika, że y − x > 0 , więc a (y − x) > 0 . Stąd licznik
rozważanego ułamka jest dodatni. W rezultacie otrzymana nierówność jest prawdziwa.
To kończy dowód.
II sposób
Z założenia wynika, że y > 0 , x > 0 i a > 0 . Zatem y + a > 0 . Mnożąc obie strony nierówności
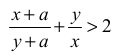
przez liczbę dodatnią (y + a)x , otrzymujemy
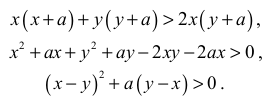
Ta nierówność jest prawdziwa, gdyż (x − y)2 > 0 oraz a(y − x) > 0 , bo z założenia x < y i a > 0 . To kończy dowód.
III sposób
Wykażemy najpierw, że jeżeli licznik i mianownik ułamka większego od 1 zwiększymy o tę samą liczbę dodatnią, to otrzymamy ułamek mniejszy od wyjściowego, gdyż przy założeniu, że liczby x, y i a są dodatnie, nierówność
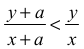
jest równoważna kolejno nierównościom
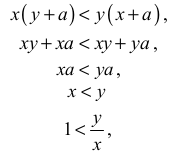
co jest prawdą.
Zatem
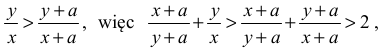
gdyż suma liczby dodatniej i jej odwrotności jest co najmniej równa 2. Ta równość zachodzi wtedy i tylko wtedy, gdy tą liczbą jest 1, co w naszym przypadku nie zachodzi, bo równość
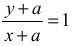
oznaczałaby, że x = y , co jest sprzeczne z założeniem x < y .
IV sposób
Niech
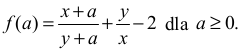
Obliczamy
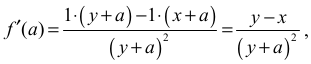
zatem ƒ′(a) > 0 dla każdego a ≥ 0 , więc ƒ jest funkcją rosnącą. Wobec tego jeśli a > 0 , to
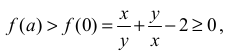
bo suma liczby dodatniej i jej odwrotności jest równa co najmniej 2.
Uwagi:
1. Prawdziwość nierówności
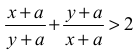
można też uzasadnić, odwołując się do nierówności między średnią arytmetyczną i geometryczną różnych liczb dodatnich
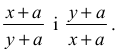
2. Uzasadnienie, że funkcja ƒ jest rosnąca w przedziale ⟨0, +∞) możemy przeprowadzić bez odwoływania się do rachunku pochodnych. Rozwiązanie może wyglądać następująco.
Niech x i y będą dowolnymi dodatnimi liczbami rzeczywistymi takimi, że x < y . Rozważmy funkcję ƒ określoną wzorem
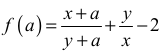
dla każdej liczby rzeczywistej a ≠ − y.
Jest to funkcja homograficzna. Zapiszmy jej wzór w postaci kanonicznej
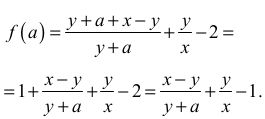
Wykresem tej funkcji jest hiperbola, której asymptotą poziomą jest, w układzie współrzędnych aOb, prosta o równaniu 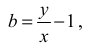
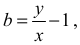 natomiast asymptotą pionową jest prosta o równaniu a = − y . Ponieważ y > x > 0 , więc
natomiast asymptotą pionową jest prosta o równaniu a = − y . Ponieważ y > x > 0 , więc 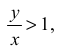 co oznacza, że asymptota pozioma leży w I i II ćwiartce układu współrzędnych, zaś asymptota pionowa leży w II i III ćwiartce tego układu.
co oznacza, że asymptota pozioma leży w I i II ćwiartce układu współrzędnych, zaś asymptota pionowa leży w II i III ćwiartce tego układu.
Ponadto x − y < 0 , więc hiperbola, która jest wykresem funkcji ƒ jest obrazem hiperboli o równaniu 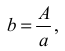 gdzie A < 0 , leżącej w II i IV ćwiartce układu współrzędnych, jak na poniższym rysunku.
gdzie A < 0 , leżącej w II i IV ćwiartce układu współrzędnych, jak na poniższym rysunku.
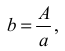 gdzie A < 0 , leżącej w II i IV ćwiartce układu współrzędnych, jak na poniższym rysunku.
gdzie A < 0 , leżącej w II i IV ćwiartce układu współrzędnych, jak na poniższym rysunku.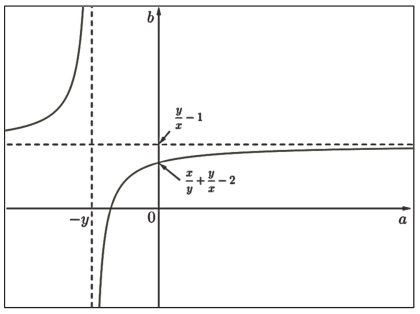
Wynika stąd, że w przedziale (−y , +∞) funkcja ƒ jest rosnąca. W szczególności jest ona rosnąca w przedziale ⟨0, +∞) . Zatem dla każdego argumentu a > 0 prawdziwa jest nierówność ƒ(a)>ƒ(0). Zauważmy, że
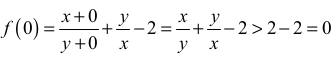
gdyż liczby 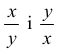 są dodatnie, różne od 1 i jedna z nich jest odwrotnością drugiej.
są dodatnie, różne od 1 i jedna z nich jest odwrotnością drugiej.
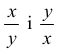 są dodatnie, różne od 1 i jedna z nich jest odwrotnością drugiej.
są dodatnie, różne od 1 i jedna z nich jest odwrotnością drugiej.W efekcie dla każdego argumentu a > 0 prawdziwa jest nierówność
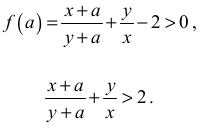
V sposób
Nierówność
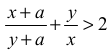
możemy przekształcić w sposób równoważny mnożąc obustronnie przez x(y + a) , bo z założenia x(y + a) jest większe od zera. Otrzymujemy
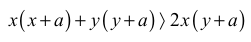
Przekształcamy otrzymaną nierówność
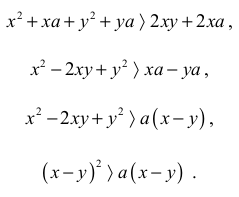
Z założenia x < y i a > 0 , zatem a(x − y) > 0 , natomiast kwadrat (x − y)2 jest dodatni.
W rezultacie otrzymana nierówność jest prawdziwa. To kończy dowód.
schemat punktacji
Rozwiązanie pełne 3 p.
Zdający przeprowadzi pełne rozumowanie.
Pokonanie zasadniczych trudności zadania 2 p.
Zdający
• zapisze nierówność w postaci równoważnej:
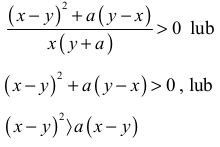
albo
• zapisze, że wystarczy wykazać prawdziwość nierówności
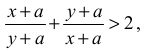
wykazując wcześniej prawdziwość nierówności
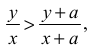
albo
• zapisze, że ƒ′ (a)>0 dla każdego a≥0 , a ponadto zbada monotoniczność funkcji ƒ i stwierdzi, że funkcja ƒ jest rosnąca,
albo
• zapisze, że wykresem funkcji
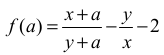
określonej dla a ≠ − y jest hiperbola, której asymptotą poziomą jest, w układzie współrzędnych aOb, prosta o równaniu
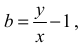
natomiast asymptotą pionową jest prosta o równaniu a = − y oraz zapisze, że
x
w przedziale ⟨0,+∞) funkcja ƒ jest rosnąca.
Rozwiązanie, w którym jest istotny postęp 1 p.
Zdający
• zapisze nierówność w postaci równoważnej:
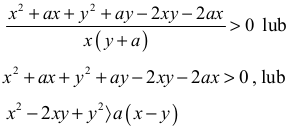
albo
• wykaże, że dla dowolnych liczb 0 < x < y i a > 0 prawdziwa jest nierówność
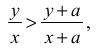
albo
• wyznaczy pochodną funkcji
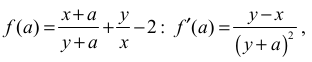
albo
• zapisze, że wykresem funkcji
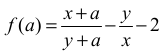
określonej dla a ≠ − y jest hiperbola , której asymptotą poziomą jest, w układzie współrzędnych aOb, prosta o równaniu
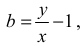
natomiast asymptotą pionową jest prosta o równaniu a = − y .