Wszystkich liczb spełniających warunki zadania jest tyle, ile permutacji zbioru 5-elementowego, czyli 5!=120 liczb.

Zapisując te liczby, jedna pod drugą, można zauważyć, że każda z cyfr – 1, 3, 5, 7, 9 – pojawia się w każdej kolumnie dokładnie 24 razy.

24 ⋅ ( 1 + 3 + 5 + 7 + 9 ) = 24 ⋅ 25 = 600.

10 ⋅ 24 ⋅ ( 1 + 3 + 5 + 7 + 9 ) = 10 ⋅ 24 ⋅ 25 = 6000.

100 ⋅ 24 ⋅ ( 1 + 3 + 5 + 7 + 9 ) = 100 ⋅ 24 ⋅ 25 = 60000.

1000 ⋅ 24 ⋅ ( 1 + 3 + 5 + 7 + 9 ) = 1000 ⋅ 24 ⋅ 25 = 600000.

10000 ⋅ 24 ⋅ ( 1 + 3 + 5 + 7 + 9 ) = 10000 ⋅ 24 ⋅ 25 = 6000000.

Zatem suma wszystkich rozważanych liczb jest równa 6666600.

(10000 + 1000 + 100 + 10 + 1) ⋅ (1 + 3 + 5 + 7 + 9) ⋅ 24 = 11111 ⋅ 25 ⋅ 24 = 6666600

Wszystkich liczb spełniających warunki zadnia jest tyle, ile permutacji zbioru 5-elementowego, czyli 5!=120 liczb.

Wśród nich są 24 liczby, w których na pierwszej pozycji znajduje się cyfra 1.

Obliczymy ich sumę:
10000 ⋅ 24 + 6 ⋅ 3000 + 6 ⋅ 5000 + 6 ⋅ 7000 + 6 ⋅ 9000 + 6 ⋅ 300 + 6 ⋅ 500 + 6 ⋅ 700 + 6 ⋅ 900 +  6 ⋅ 30 + 6 ⋅ 50 + 6 ⋅ 70 + 6 ⋅ 90 + 6 ⋅ 3 + 6 ⋅ 5 + 6 ⋅ 7 + 6 ⋅ 9 = 399984

Rozważmy następnie 24 liczby, w których na pierwszej pozycji znajduje się cyfra 3.
Obliczymy ich sumę:

30000 ⋅ 24 + 6 ⋅ 1000 + 6 ⋅ 5000 + 6 ⋅ 7000 + 6 ⋅ 9000 + 6 ⋅ 100 + 6 ⋅ 500 + 6 ⋅ 700 + 6 ⋅ 900 + 6 ⋅ 10 + 6 ⋅ 50 + 6 ⋅ 70 + 6 ⋅ 90 + 6 ⋅ 1 + 6 ⋅ 5 + 6 ⋅ 7 + 6 ⋅ 9 = 866652

Rozważmy z kolei 24 liczby, w których na pierwszej pozycji znajduje się 5.
Obliczymy ich sumę:
50000 ⋅ 24 + 6 ⋅ 1000 + 6 ⋅ 3000 + 6 ⋅ 7000 + 6 ⋅ 9000 + 6 ⋅ 100 + 6 ⋅ 300 + 6 ⋅ 700 + 6 ⋅ 900 + 6 ⋅ 10 + 6 ⋅ 30 + 6 ⋅ 70 + 6 ⋅ 90 + 6 ⋅ 1 + 6 ⋅ 3 + 6 ⋅ 7 + 6 ⋅ 9 = 1333320

Rozważmy z kolei 24 liczby, w których na pierwszej pozycji znajduje się cyfra 7.
Obliczymy ich sumę:
70000 ⋅ 24 + 6 ⋅ 1000 + 6 ⋅ 3000 + 6 ⋅ 5000 + 6 ⋅ 9000 + 6 ⋅ 100 + 6 ⋅ 300 + 6 ⋅ 500 + 6 ⋅ 900 + 6 ⋅ 10 + 6 ⋅ 30 + 6 ⋅ 50 + 6 ⋅ 90 + 6 ⋅ 1 + 6 ⋅ 3 + 6 ⋅ 5 + 6 ⋅ 9 = 1799988

Rozważmy wreszcie 24 liczby, w których na pierwszej pozycji znajduje się cyfra 9.
Obliczymy ich sumę:
90000 ⋅ 24 + 6 ⋅ 1000 + 6 ⋅ 3000 + 6 ⋅ 5000 + 6 ⋅ 7000 + 6 ⋅ 100 + 6 ⋅ 300 + 6 ⋅ 500 + 6 ⋅ 700 + 6 ⋅ 10 + 6 ⋅ 30 + 6 ⋅ 50 + 6 ⋅ 70 + 6 ⋅ 1 + 6 ⋅ 3 + 6 ⋅ 5 + 6 ⋅ 7 = 2266656

Zatem suma wszystkich rozważanych liczb jest równa 6666600 .

Wszystkich liczb spełniających warunki zadnia jest tyle, ile permutacji zbioru 5-elementowego, czyli 5!=120 liczb.

Wśród nich jest 12 liczb, w których na pierwszych dwóch pozycjach stoją cyfry 1 i 3.
Obliczymy ich sumę:
10000 ⋅ 6 + 30000 ⋅ 6 + 1000 ⋅ 6 + 3000 ⋅ 6 + 4 ⋅ 500 + 4 ⋅ 50 + 4 ⋅ 5 + 4 ⋅ 700 + 4 ⋅ 70 + 4 ⋅ 7 + 4 ⋅ 900 + 4 ⋅ 90 + 4 ⋅ 9 = 273324.

Rozważmy następnie 12 liczb, w których na pierwszych dwóch pozycjach stoją cyfry 1 i 5.
Obliczymy ich sumę:
10000 ⋅ 6 + 50000 ⋅ 6 + 1000 ⋅ 6 + 5000 ⋅ 6 + 4 ⋅ 300 + 4 ⋅ 30 + 4 ⋅ 3 + 4 ⋅ 700 + 4 ⋅ 70 + 4 ⋅ 7 + 4 ⋅ 900 + 4 ⋅ 90 + 4 ⋅ 9 = 404436.

Rozważmy następnie 12 liczb, w których na pierwszych dwóch pozycjach stoją cyfry 1 i 7.
Obliczymy ich sumę:
10000 ⋅ 6 + 70000 ⋅ 6 + 1000 ⋅ 6 + 7000 ⋅ 6 + 4 ⋅ 300 + 4 ⋅ 30 + 4 ⋅ 3 + 4 ⋅ 500 + 4 ⋅ 50 + 4 ⋅ 5 + 4 ⋅ 900 + 4 ⋅ 90 + 4 ⋅ 9 = 535548.

Rozważmy następnie 12 liczb, w których na pierwszych dwóch pozycjach stoją cyfry 1 i 9.
Obliczymy ich sumę:
10000 ⋅ 6 + 90000 ⋅ 6 + 1000 ⋅ 6 + 9000 ⋅ 6 + 4 ⋅ 300 + 4 ⋅ 30 + 4 ⋅ 3 + 4 ⋅ 500 + 4 ⋅ 50 + 4 ⋅ 5 + 4 ⋅ 700 + 4 ⋅ 70 + 4 ⋅ 7 = 666660.

Rozważmy z kolei 12 liczb, w których na pierwszych dwóch pozycjach stoją cyfry 3 i 5.
Obliczymy ich sumę:
30000 ⋅ 6 + 50000 ⋅ 6 + 3000 ⋅ 6 + 5000 ⋅ 6 + 4 ⋅ 100 + 4 ⋅ 10 + 4 ⋅ 1 + 4 ⋅ 900 + 4 ⋅ 90 + 4 ⋅ 9 + 4 ⋅ 700 + 4 ⋅ 70 + 4 ⋅ 7 = 535548.

Rozważmy następnie 12 liczb, w których na pierwszych dwóch pozycjach stoją cyfry 3 i 7.
Obliczymy ich sumę:
30000 ⋅ 6 + 70000 ⋅ 6 + 3000 ⋅ 6 + 7000 ⋅ 6 + 4 ⋅ 100 + 4 ⋅ 10 + 4 ⋅ 1 + 4 ⋅ 500 + 4 ⋅ 50 + 4 ⋅ 5 + 4 ⋅ 900 + 4 ⋅ 90 + 4 ⋅ 9 = 666660.

Rozważmy następnie 12 liczb, w których na pierwszych dwóch pozycjach stoją cyfry 3 i 9.
Obliczymy ich sumę:

30000 ⋅ 6 + 90000 ⋅ 6 + 3000 ⋅ 6 + 9000 ⋅ 6 + 4 ⋅ 100 + 4 ⋅ 10 + 4 ⋅ 1 + 4 ⋅ 500 + 4 ⋅ 50 + 4 ⋅ 5 + 4 ⋅ 700 + 4 ⋅ 70 + 4 ⋅ 7 = 797772.

Rozważmy następnie 12 liczb, w których na pierwszych dwóch pozycjach stoją cyfry 5 i 7.
Ich suma jest taka sama jak w poprzednim przypadku: 797772 .
Rozważmy z kolei 12 liczb, w których na pierwszych dwóch pozycjach stoją cyfry 5 i 9.
Obliczymy ich sumę:
90000 ⋅ 6 + 50000 ⋅ 6 + 9000 ⋅ 6 + 5000 ⋅ 6 + 4 ⋅ 100 + 4 ⋅ 10 + 4 ⋅ 1 + 4 ⋅ 300 + 4 ⋅ 30 + 4 ⋅ 3 + 4 ⋅ 700 + 4 ⋅ 70 + 4 ⋅ 7 = 928884.

Rozważmy wreszcie 12 liczb, w których na pierwszych dwóch pozycjach stoją cyfry 7 i 9.
Obliczymy ich sumę:
90000 ⋅ 6 + 70000 ⋅ 6 + 9000 ⋅ 6 + 7000 ⋅ 6 + 4 ⋅ 100 + 4 ⋅ 10 + 4 ⋅ 1 + 4 ⋅ 300 + 4 ⋅ 30 + 4 ⋅ 3 + 4 ⋅ 500 + 4 ⋅ 50 + 4 ⋅ 5 = 1059996.

Zatem suma wszystkich rozważanych liczb jest równa 6666600 .

Zauważmy, że zbiór wszystkich 120 liczb pięciocyfrowych uzyskanych z cyfr 1, 3, 5, 7, 9 można pogrupować w pary takie, że suma cyfr w rzędach jedności, dziesiątek, setek, tysięcy, i dziesiątek tysięcy jest równa 10, np. 37195 i 73915. Suma każdej takiej pary liczb jest równa 111110. Takich par liczb jest ½·5!=60.

Stąd szukana suma jest równa 6666600 .

Przy dodawaniu rozważanych liczb wykorzystamy fakt, że:

- cyfry 1, 3, 5, 7, 9 stojące w rzędzie jedności
oznaczają odpowiednio dodawanie liczb 1, 3, 5, 7, 9;
- cyfry 1, 3, 5, 7, 9 stojące w rzędzie dziesiątek
oznaczają odpowiednio dodawanie liczb 10, 30, 50, 70, 90;
- cyfry 1, 3, 5, 7, 9 stojące w rzędzie setek
oznaczają odpowiednio dodawanie liczb 100, 300, 500, 700, 900;
- cyfry 1, 3, 5, 7, 9 stojące w rzędzie tysięcy
oznaczają odpowiednio dodawanie liczb 1000, 3000, 5000, 7000, 9000;
- cyfry 1, 3, 5, 7, 9 stojące w rzędzie dziesiątek tysięcy
oznaczają odpowiednio dodawanie liczb 10000, 30000, 50000, 70000, 90000.

Obliczenie sumy
1 + 3 + 5 + 7 + 9 + 10 + 30 + 50 + 70 + 90 + 100 + 300 + 500 + 700 + 900 + 1000 + 3000 + 5000 + 7000 + 9000 + 10000 + 30000 + 50000 + 70000 + 90000 = 277775
jest równoznaczne z obliczeniem sumy pięciu z rozważanych liczb, przy czym te pięć liczb charakteryzuje własność: w tych pięciu liczbach każda cyfra zajmuje dokładnie 1 raz każdą z pięciu możliwych pozycji w liczbie pięciocyfrowej.

Odpowiednie przestawianie cyfr pozwoli rozdzielić zbiór wszystkich rozważanych w zadaniu liczb na 4! rozłącznych podzbiorów 5-elementowych, przy czym w każdym z tych podzbiorów suma wszystkich 5 liczb będzie równa 277775.

Zatem suma wszystkich rozważanych w zadaniu liczb jest równa:

4! ⋅ 277775 = 6666600.

Zdający zapisze, że suma wszystkich rozważanych liczb jest równa 6666600 .

Zdający

• zapisze, że należy dodać do siebie 120 liczb, a w tych liczbach na każdej pozycji liczby 5-cyfrowej każda cyfra ze zbioru {1,3,5,7,9} pojawi się dokładnie 24 razy i na tym zakończy lub popełni błędy,

albo

• obliczy dla wszystkich 120 liczb poprawną sumę tych samych pozycji systemu dziesiątkowego, tzn. sumę wszystkich jedności lub wszystkich dziesiątek, lub wszystkich setek, lub wszystkich tysięcy, lub wszystkich dziesiątek tysięcy i na tym zakończy lub popełni błędy,

albo

• obliczy sumę 24 liczb, mających na ustalonej pozycji systemu dziesiątkowego tę samą cyfrę i na tym zakończy lub popełni błędy,

albo

• obliczy przynajmniej 4 sumy 12 liczb, takich, że w sumowanych dwunastu liczbach na ustalonych dwóch pozycjach występuje ta sama para liczb i na tym zakończy lub popełni błędy,

albo

• zauważy i zapisze, że zbiór wszystkich 120 liczb pięciocyfrowych uzyskanych z cyfr 1, 3, 5, 7, 9 można pogrupować w pary takie, że suma cyfr w rzędach jedności, dziesiątek, setek, tysięcy, i dziesiątek tysięcy jest równa 10 i na tym zakończy lub popełni błędy,

albo

• obliczy sumę pięciu liczb o własności: w tych pięciu liczbach każda cyfra zajmuje dokładnie 1 raz każdą z pięciu możliwych pozycji w liczbie pięciocyfrowej: 277775 i ponadto zauważy, że zbiór wszystkich rozważanych w zadaniu liczb można rozdzielić na 4! rozłącznych podzbiorów 5-elementowych, charakteryzujących się tym, że suma liczb z każdego podzbioru jest taka sama i na tym zakończy lub popełni błędy.

Zdający

• zapisze, że wszystkich pięciocyfrowych liczb o różnych cyfrach utworzonych z cyfr 1, 3, 5, 7, 9 jest 120 lub je wypisze

albo

• zapisze, że któraś z cyfr występuje 24 razy na którymś z pięciu miejsc liczby pięciocyfrowej, np. cyfra 1 stoi 24 razy na pierwszej pozycji,

albo

• ustali, że na konkretnych dwóch pozycjach liczby pięciocyfrowej można ustawić cyfry ze zbioru { 1, 3, 5, 7, 9 } na 20 sposobów lub do ustawienia na konkretnych dwóch pozycjach liczby pięciocyfrowej można wybrać dwie liczby ze zbioru { 1, 3, 5, 7, 9 } na 10 sposobów,

albo

• obliczy sumę pięciu liczb o własności: w tych pięciu liczbach każda cyfra zajmuje dokładnie 1 raz każdą z pięciu możliwych pozycji w liczbie pięciocyfrowej: 277775,

albo

• zauważy, że zbiór wszystkich rozważanych w zadaniu liczb można rozdzielić na 4! rozłącznych podzbiorów 5-elementowych, charakteryzujących się tym, że suma liczb z każdego podzbioru jest taka sama.

1. Jeżeli zdający oblicza sumę

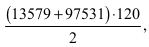
bez stosownego komentarza lub bez wypisania dwóch par liczb takich, że w każdej parze suma cyfr w rzędach jedności, dziesiątek, setek, tysięcy, i dziesiątek tysięcy jest równa 10, to otrzymuje 1 punkt.

2. Jeżeli zdający rozważa zamiast cyfr 1, 3, 5, 7, 9 pięć różnych cyfr, przy czym co najmniej jedna z nich nie należy do zbioru {1, 3, 5, 7, 9} i konsekwentnie rozwiąże zadanie do końca, to może otrzymać co najwyżej 2 punkty.

3. Jeżeli zdający zlicza sumę liczb przyjmując, że cyfry 1, 3, 5, 7, 9 mogą się powtarzać i konsekwentnie rozwiąże zadanie do końca, to może otrzymać co najwyżej 1 punkt.