Odpowiedź:
Przykładowe rozwiązanie
Przyjmijmy oznaczenia jak na rysunku.
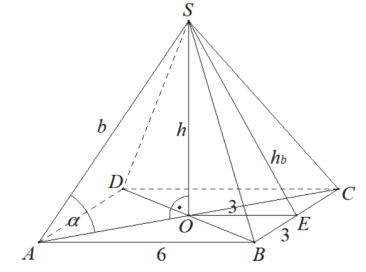
Ze wzoru na długość przekątnej kwadratu otrzymujemy
Pole podstawy ostrosłupa jest równe
Pp = 62 = 36 .
Pole powierzchni całkowitej ostrosłupa jest 4 razy większe od pola jego podstawy, więc
Pc = 4Pp = 4 ⋅ 36 = 144 .
Zatem pole powierzchni bocznej ostrosłupa jest równe
Pb = Pc − Pp = 3 ⋅ 36 = 108 .
Pole powierzchni bocznej ostrosłupa jest równe
więc
12 ⋅ hb = 108
hb = 9
Z twierdzenia Pitagorasa dla trójkąta BES otrzymujemy
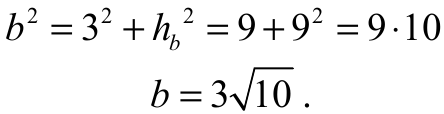
Z trójkąta AOS otrzymujemy
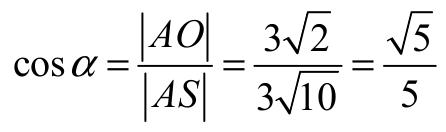
schemat punktacji
Rozwiązanie pełne 5 p.
Zdający obliczy cosinus kąta nachylenia krawędzi bocznej do płaszczyzny podstawy:
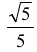
Rozwiązanie prawie pełne 4 p.
Zdający
Zdający
• obliczy długość krawędzi bocznej ostrosłupa: b = 3√10
albo
• obliczy tgα
i na tym zakończy lub dalej popełni błędy.
i na tym zakończy lub dalej popełni błędy.
Pokonanie zasadniczych trudności zadania 3 p.
Zdający obliczy wysokość ściany bocznej ostrosłupa: hb = 9 .
i na tym zakończy lub dalej popełni błędy.
Zdający obliczy wysokość ściany bocznej ostrosłupa: hb = 9 .
i na tym zakończy lub dalej popełni błędy.
Rozwiązanie, w którym jest istotny postęp 2 p.
Zdający zapisze równanie pozwalające obliczyć wysokość ściany bocznej, np.:
Zdający zapisze równanie pozwalające obliczyć wysokość ściany bocznej, np.:
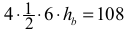
Rozwiązanie, w którym postęp jest niewielki, ale konieczny na drodze do pełnego rozwiązania 1 p.
Zdający
• zapisze zależność pomiędzy polem powierzchni bocznej a polem podstawy lub pomiędzy polem ściany bocznej a polem podstawy, np.:
Zdający
• zapisze zależność pomiędzy polem powierzchni bocznej a polem podstawy lub pomiędzy polem ściany bocznej a polem podstawy, np.:
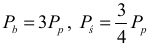
albo
• zapisze dwa równania: Pc = 4Pp i Pc = Pp + Pb ,
albo
• obliczy pole powierzchni bocznej ostrosłupa: Pb = 108 ,
albo
• zapisze, że
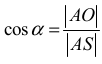
albo
obliczy długość przekątnej podstawy ostrosłupa lub połowę jej długości: |AC|=6√2 lub |AO|=3√2