Odpowiedź:
Przykładowe rozwiązania
I sposób
Przekształcamy równoważnie nierówność i otrzymujemy kolejno:
3a2 − 2ab + 3b2 ≥ 0 ,
2a2 + a2 − 2ab + b2 + 2b2 ≥ 0 ,
2a2 + (a − b)2 + 2b2 ≥ 0 .
2a2 + a2 − 2ab + b2 + 2b2 ≥ 0 ,
2a2 + (a − b)2 + 2b2 ≥ 0 .
Lewa strona nierówności jest sumą trzech liczb nieujemnych:
2a2 – jako wielokrotność kwadratu liczby,
(a − b)2 – jako kwadrat liczby,
2b2 – jako wielokrotność kwadratu liczby.
Zatem
z lewej strony nierówności występuje wyrażenie przyjmujące wartość
nieujemną, czyli nierówność jest prawdziwa dla dowolnych rzeczywistych
liczb a i b.
To kończy dowód.
Uwaga
Całe rozumowanie można zapisać w postaci
Całe rozumowanie można zapisać w postaci
3a2 − 2ab + 3b2 ≥ a2 − 2ab + b2 =
= (a − b)2 ≥ 0,
co jest prawdą dla dowolnych liczb rzeczywistych a, b.
II sposób
Przekształcamy równoważnie nierówność i otrzymujemy kolejno:
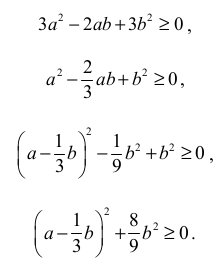
Lewa strona nierówności jest sumą dwóch liczb nieujemnych:
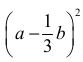– jako kwadrat liczby,
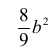– jako wielokrotność kwadratu liczby.Zatem
z lewej strony nierówności występuje wyrażenie przyjmujące wartość
nieujemną, czyli nierówność jest prawdziwa dla dowolnych rzeczywistych
liczb a i b.
To kończy dowód.
III sposób
Wyrażenie
z lewej strony jest trójmianem kwadratowym dla zmiennej a, z parametrem
b. Obliczamy wyróżnik tego trójmianu kwadratowego:
Δ = (− 2b)2 − 4 ⋅ 3 ⋅ 3b2 = 4b2 − 36b2 = − 32b2 .
To kończy dowód.
IV sposób
Rozważmy dwa przypadki.
1. b = 0
2. b ≠ 0
1. b = 0
2. b ≠ 0
W pierwszym przypadku otrzymujemy nierówność 3a2
≥ 0 , która jest prawdziwa dla dowolnej liczby rzeczywistej a, bo
wyrażenie po lewej stronie jest wielokrotnością kwadratu liczby.
Zatem nierówność 3a2 − 2ab + 3b2 ≥ 0 jest prawdziwa w przypadku, gdy b = 0 .
W drugim przypadku możemy podzielić obie strony nierówności 3a2 − 2ab + 3b2 ≥ 0 przez b2 .
Otrzymujemy nierówność:
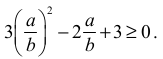
Obliczamy wyróżnik trójmianu kwadratowego zmiennej x, gdzie x = a⁄b, występującego z lewej strony nierówności:
Δ = (−2)2 − 4 ⋅ 3 ⋅ 3 = 4 − 36 = −32 .
Obliczony wyróżnik trójmianu kwadratowego jest ujemny, zatem trójmian kwadratowy nie ma
pierwiastków rzeczywistych. Przy najwyższej potędze trójmianu kwadratowego stoi liczba
dodatnia 3, zatem lewa strona nierówności przyjmuje zawsze wartość dodatnią. Oznacza to, że
nierówność jest prawdziwa dla dowolnej liczby a i dowolnej liczby b różnej od zera.
Z rozważonych dwóch przypadków wynika, że nierówność jest prawdziwa dla dowolnych rzeczywistych liczb a i b.
To kończy dowód.
V sposób (przypadki ze względu na znak ab).
Rozważmy dwa przypadki.
1. Gdy ab ≤ 0 . Wtedy nierówność 3a2 − 2ab + 3b2 ≥ 0 jest prawdziwa, gdyż po jej lewej stronie jest suma trzech nieujemnych składników 3a2 , 2ab , 3b2
2. Gdy ab > 0 . Wtedy nierówność zapisujemy w postaci równoważnej 3a2 + 3b2 ≥ 2ab.
Obie strony tej nierówności możemy wtedy podzielić przez dodatnią liczbę 3ab , otrzymując nierówność
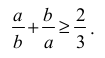
Z twierdzenia o sumie liczby dodatniej i jej odwrotności wynika, że
To kończy dowód.
VI sposób (dowód nie wprost)
Załóżmy, nie wprost, że dla pewnych liczb rzeczywistych a i b prawdziwa jest nierówność
3a2 − 2ab + 3b2 < 0
Ponieważ 2a2 + 2b2 ≥ 0 , więc nierówność ta byłaby prawdziwa tylko wtedy,
gdyby a2 − 2ab + b2 < 0 ,
czyli (a − b)2 < 0 , co jest nieprawdą.
Otrzymana sprzeczność oznacza,
że nierówność 3a2 − 2ab + 3b2 < 0 jest fałszywa.
Prawdziwa zatem jest nierówność:
3a2 − 2ab + 3b2 ≥ 0
To kończy dowód.
VII sposób
Dla dowolnych liczb rzeczywistych a, b prawdziwe są nierówności
(a − b)2 ≥ 0 oraz 2a2 + 2b2 ≥ 0 ,
czyli
a2 − 2ab + b2 ≥ 0 oraz 2a2 + 2b2 ≥ 0 .
Dodając te nierówności stronami, co możemy zrobić, gdyż nierówności są tak samo skierowane, otrzymujemy
a2 − 2ab + b2 + 2a2 + 2b2 ≥ 0
czyli
3a2 − 2ab + 3b2 ≥ 0
To kończy dowód.
schemat punktacji
Zdający otrzymuje 2 p.
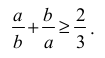
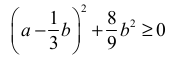
gdy przeprowadzi pełne rozumowanie.
Zdający otrzymuje 1 p.
gdy
gdy
• zapisze nierówność w postaci, zawierającej po jednej stronie 0, a po drugiej sumę
wyrażeń algebraicznych, będących wielokrotnościami kwadratów liczb lub
stanowiących jedną stronę wzoru skróconego mnożenia, którego druga strona jest
kwadratem, np.:
2 a2 + a2 − 2 ab + b2 + 2b2 ≥ 0
albo
• zapisze oszacowanie
3a2 − 2ab + 3b2 ≥ a2 − 2 ab + b2
albo
• obliczy wyróżnik trójmianu kwadratowego w zależności od zmiennej a lub b,
występującego po jednej stronie nierówności, gdy po drugiej stronie jest 0, i stwierdzi,
że jest on niedodatni
albo
• rozważa dwa przypadki: w pierwszym stwierdza, że gdy ab ≤ 0 , to nierówność jest prawdziwa, a drugim doprowadza nierówność do postaci
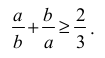
albo
rozważa dwa przypadki: w jednym dzieli stronami nierówność przez b2 lub przez a2 ,
a w drugim przyjmuje, że a lub b jest równe 0, oraz w przypadku, w którym dzieli
stronami nierówność i obliczy wyróżnik otrzymanego trójmianu kwadratowego,
albo
• zapisze, że prawdziwa jest nierówność 2a2 + 2b2 ≥ 0 oraz zapisze, że prawdziwa jest nierówność (a−b)2 ≥ 0 i przedstawi tę nierówność w postaci równoważnej a2 − 2ab + b2 ≥ 0
albo
• wskaże, że przeprowadza dowód nie wprost, zapisze nierówność 3a2 − 2ab + 3b2 < 0oraz zapisze jeden z dwóch poniższych komentarzy:
- nierówność ( a − b )2 < 0 jest nieprawdziwa;
- nierówność ( a − b )2 ≥ 0 jest prawdziwa oraz nierówność 2a2 + 2b2 < 0 jest nieprawdziwa
i na tym zakończy lub dalej popełnia błędy.
Uwagi:
1. Jeżeli zdający sprawdza prawdziwość nierówności jedynie dla wybranych wartości a i b, to otrzymuje 0 punktów za całe rozwiązanie.
2. Jeżeli zdający zakończy rozumowanie, zapisując nierówność
2a2 + ( a − b ) + 2b2 ≥ 0 lub
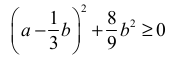
i nie przedstawi komentarza uzasadniającego przyjmowanie wyłącznie nieujemnych wartości przez wyrażenie zapisane po lewej stronie nierówności, to otrzymuje 1 punkt.
3. Jeżeli zdający w IV sposobie rozwiązania pominie przypadek b = 0 lub a = 0 , to za całe
rozwiązanie może otrzymać co najwyżej 1 punkt.
4. Jeżeli zdający w V sposobie rozwiązania pominie przypadek ab ≤ 0 , to za całe rozwiązanie
może otrzymać co najwyżej 1 punkt, o ile wykaże prawdziwość nierówności w przypadku
ab > 0 .
5. Jeżeli zdający po uzasadnieniu prawdziwości nierówności a2 − 2ab + b2 ≥ 0 zapisze nierówność 3a2 − 2ab + 3b2 ≥ 0 i na tym zakończy, to za całe rozwiązanie otrzymuje 1 punkt.