Odpowiedź:
Przykładowe rozwiązanie
Niech a1 będzie pierwszym wyrazem ciągu geometrycznego, zaś q jego ilorazem.
Z treści zadania otrzymujemy układ równań:
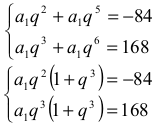
Dzieląc stronami te równania, co możemy zrobić, gdyż gdyby którakolwiek z liczb a1 , q , 1 + q3 była równa 0, to otrzymalibyśmy sprzeczność, otrzymujemy
q = −2 .
q = −2 .
Zatem
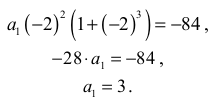
Otrzymaliśmy ciąg geometryczny (an) , w którym:
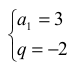
Wykorzystując wzór na sumę n początkowych wyrazów ciągu geometrycznego, doprowadzamy do równania postaci
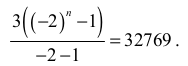
Przekształcając to równanie, otrzymujemy (−2)n = −32768 .
Ponieważ (−2)n = (−2)15 , więc n = 15 .
schemat punktacji
Rozwiązanie, w którym postęp jest niewielki, ale konieczny na drodze do pełnego
rozwiązania 1 p.
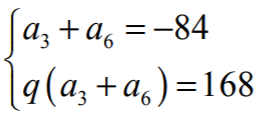
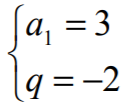
Zdający zapisze
• układ równań z dwiema niewiadomymi, np.:

albo
• układ równań z niewiadomymi q, a3, a6, np.:
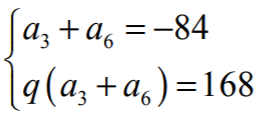
i na tym zakończy lub dalej popełnia błędy.
Rozwiązanie, w którym jest istotny postęp 2 p.
Zdający zapisze równanie z jedną niewiadomą a1 lub q
i na tym zakończy lub dalej popełnia błędy.
Pokonanie zasadniczych trudności 3 p.
Zdający rozwiąże układ równań:
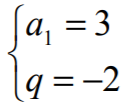
Rozwiązanie pełne 4 p.
Zdający wyznaczy szukaną liczbę n:
n = 15
Uwagi
1. Jeżeli zdający przedstawi poprawną strategię poszukiwania liczby n, ale otrzyma błędne
wartości a1 lub q, takie że po podstawieniu do wzoru na Sn otrzymuje równanie, którego
rozwiązanie nie jest liczbą naturalną, to może otrzymać co najwyżej 2 punkty, za
realizację rozwiązania do etapu: istotny postęp.
2. Jeżeli zdający zapisze q = −2 bez rozwiązania układu lub stosownego uzasadnienia, to
może otrzymać co najwyżej 2 punkty.
3. Jeżeli zdający korzysta przy wyznaczaniu n z zapisanej przez siebie zależności
"−(−2)n = 2n"
bez stosownego komentarza, to może otrzymać co najwyżej 3 punkty.