Odpowiedź:
Przykładowe rozwiązanie
Przekrojem osiowym stożka jest trapez równoramienny ABCD. Niech DE oznacza wysokość stożka opuszczoną z punktu D.
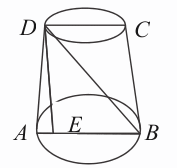
Po podstawieniu danych do wzoru na objętość otrzymujemy równanie kwadratowe
1⁄3 π ⋅ 10 ⋅ (62 + 6R + R2) = 840π
Stąd
R2 + 6R − 216 = 0 .
Rozwiązując je, otrzymujemy
Δ = 36 + 4 ⋅ 216 = 900, Δ = 30 ,
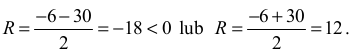
Przekrojem osiowym tego stożka jest trapez równoramienny o podstawach długości 24 i 12 oraz wysokości 10. Długość odcinka EB jest równa
|EB| = R + r = 12 + 6 = 18 .
Z twierdzenia Pitagorasa dla trójkąta BDE otrzymujemy
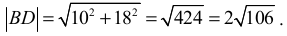
Zatem
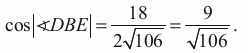
schemat punktacji
Rozwiązanie, w którym postęp jest niewielki, ale konieczny na drodze do pełnego
rozwiązania 1 p.
Zdający wyznaczy promień R większej podstawy: R = 12 i na tym zakończy lub dalej popełni
błędy.
Rozwiązanie, w którym jest istotny postęp 2 p.
Zdający wyznaczy promień R większej podstawy: R = 12 i długość odcinka EB:
|EB| = 18
i na tym zakończy lub dalej popełni błędy.
Pokonanie zasadniczych trudności zadania 3 p.
Zdający obliczy
• długość przekątnej trapezu |BD| = 2√106
albo
• obliczy tangens kąta DBE:
tg |∢DBE| = 5⁄9
i na tym zakończy lub dalej popełni błędy.
Rozwiązanie pełne 4 p.
Zdający obliczy 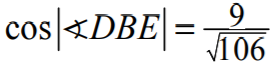
Uwagi
1. Jeżeli zdający zapisze cosinus kąta nachylenia przekątnej przekroju osiowego tego
stożka ściętego do jednej z jego podstaw w zależności od R, r, H i na tym zakończy
lub dalej popełnia błędy, to otrzymuje 2 punkty.
2. Jeżeli zdający popełni błąd merytoryczny przy zastosowaniu twierdzenia Pitagorasa,
pisząc np.: |EB|2 + |BD|2 = |ED|2 , albo popełni błąd merytoryczny przez zastosowanie
nieistniejącego wzoru "pierwiastek sumy = suma pierwiastków", to może otrzymać co
najwyżej 2 punkty za całe rozwiązanie.
3. Jeżeli zdający błędnie przyjmie, że wysokością stożka jest odcinek AD, to może
otrzymać co najwyżej 1 punkt, o ile poprawnie obliczy R.
4. Jeżeli zdający realizuje strategię rozwiązania zadania i popełnia jedynie błędy
rachunkowe, to może otrzymać 3 punkty, o ile popełnione błędy nie ułatwiają
rozwiązania na żadnym etapie.
5. Jeżeli zdający obliczy długość R oraz długość ramienia trapezu, to może otrzymać
2 punkty. Jeżeli zdający obliczy długość R oraz długość ramienia trapezu, a ponadto
obliczy długość BD i zapisze twierdzenie cosinusów, to może otrzymać 3 punkty.
6. Jeżeli zdający błędnie przyjmuje, że średnica górnej podstawy stożka ściętego ma
długość 6, to otrzymuje co najwyżej 3 punkty.
7. Jeżeli zdający błędnie przyjmuje, że długość rzutu prostokątnego ramienia trapezu na
dłuższą podstawę to różnica średnic dolnej i górnej podstawy zamiast połowy tej
różnicy i nie jest to błąd wynikający z rachunków, to otrzymuje co najwyżej 2 punkty
za całe rozwiązanie.