Zdarzeniami elementarnymi są permutacje (bez powtórzeń) zbioru ośmioelementowego

{ 1, 2, 3, 4, 5, 6, 7, 9 }.

Liczba wszystkich zdarzeń elementarnych jest równa

|Ω| = 8! 

Niech A będzie zdarzeniem, polegającym na tym, że żadne dwie liczby parzyste nie są sąsiednimi wyrazami utworzonego ciągu. Ustalmy liczbę wszystkich zdarzeń elementarnych sprzyjających zdarzeniu A.

W zbiorze Z jest 5 liczb nieparzystych, więc możemy je ustawić w ciąg na 5! sposobów. 

Otrzymamy wtedy sytuację:

Pierwszą z pozostałych liczb (parzystych) zbioru Z możemy ustawić na jednym z sześciu miejsc 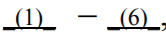 drugą na jednym z pozostałych pięciu, a trzecią na jednym z pozostałych czterech.

Zatem

|A| = 5!⋅6⋅5⋅4

W zbiorze Z jest 5 liczb nieparzystych, więc możemy je ustawić w ciąg na 5! sposobów. 

Otrzymamy wtedy sytuację:

Trzy pozostałe liczby (parzyste) ze zbioru Z musimy ustawić na wybranych trzech miejscach spośród sześciu miejsc 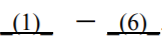. Te trzy miejsca możemy wybrać na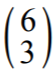sposobów. Na tych trzech ustalonych miejscach możemy trzy liczby parzyste ze zbioru Z ustawić na 3! sposobów.

Zatem

III metoda (ustalenie kolejności parzystych, a następnie ustalenie pozycji parzystych)

W zbiorze Z mamy 3 liczby parzyste: 2, 4, 6. Możemy ustawić je w kolejności na 3! = 6 sposobów. Jedną z takich możliwości jest kolejność: 2, 4, 6. Wypiszmy wszystkie przypadki ustawienia tych trzech liczb w kolejności 2, 4, 6 w ciągu 8-wyrazowym:

(a) 2 na pierwszym miejscu

(b) 2 na drugim miejscu

(c) 2 na trzecim miejscu

(d) 2 na czwartym miejscu

Łącznie mamy 20 przypadków ustawienia w ciągu 8-wyrazowym trzech liczb parzystych – 2, 4, 6 – w kolejności 2, 4, 6.

Ponieważ mamy 6 możliwości ustalenia kolejności dla trzech liczb 2, 4, 6, więc liczby parzyste ze zbioru Z możemy ustawić na 6⋅20 sposobów.

Do ustawionych liczb parzystych na wolne miejsca ustawiamy liczby nieparzyste, a możemy to zrobić na 5! sposobów.

Zatem

|A| = 6⋅20⋅5!

IV metoda (ustalenie pozycji parzystych)

Wypiszmy wszystkie przypadki wyboru trzech miejsc, spośród ośmiu, dla liczb parzystych, z uwzględnieniem warunku, że żadne dwie parzyste nie sąsiadują ze sobą

(a) pierwsza liczba parzysta na pierwszym miejscu

(b) pierwsza liczba parzysta na drugim miejscu

(c) pierwsza liczba parzysta na trzecim miejscu

(d) pierwsza liczba parzysta na czwartym miejscu

Łącznie mamy 20 przypadków ustalenia w ciągu 8-wyrazowym pozycji liczb parzystych.

Zatem

|A| = 20⋅3!⋅5!

Uwaga!

Te same przypadki wyboru uzyskamy, wypisując wszystkie ustawienia liczb parzystych i nieparzystych przy założeniu, że rozpoczynamy najpierw od liczby parzystej (10 przypadków), a następnie od nieparzystej (kolejne 10 przypadków). Ponadto należy pamiętać, że przedstawione tu przypadki ustawień liczb parzystych (a tym samym i nieparzystych) mogą być przedstawione jako gałęzie drzewa probabilistycznego z 20 gałęziami.

V metoda (przerwy między parzystymi)

Trzy liczby parzyste musimy rozdzielić pięcioma nieparzystymi, przy czym nieparzyste możemy umieszczać także przed wszystkimi parzystymi lub po wszystkich parzystych. Mamy zatem 4 usytuowania dla liczb nieparzystych. Wypiszmy najpierw przypadki uwzględniające liczbę pozycji dla liczb nieparzystych w poszczególnych usytuowaniach (cyfra oznacza liczbę miejsc zajętych przez liczby nieparzyste, litera p oznacza liczbę parzystą).

Łącznie mamy 20 takich przypadków.

Zatem

|A| = 20⋅3!⋅5!

Obliczamy prawdopodobieństwo:

Zdarzeniami elementarnymi są permutacje (bez powtórzeń) zbioru ośmioelementowego

{ 1, 2, 3, 4, 5, 6, 7, 9 }.

Liczba wszystkich zdarzeń elementarnych jest równa

|Ω| = 8!

Niech A będzie zdarzeniem, polegającym na tym, że żadne dwie liczby parzyste nie są sąsiednimi wyrazami utworzonego ciągu.

Zdarzeniem przeciwnym A′ jest otrzymanie w wyniku permutacji zbioru Z ciągu, w którym liczby parzyste są sąsiednimi wyrazami ciągu, tzn.

I: wszystkie trzy liczby parzyste będą kolejnymi wyrazami ciągu

albo

II. dwie liczby parzyste będą kolejnymi wyrazami ciągu, a trzecia liczba parzysta nie będzie sąsiadować z żadną z nich.

W sytuacji I miejsca dla liczb parzystych wybieramy na 6 sposobów, ustawiamy na tych miejscach liczby parzyste na 3! sposobów, a pozostałe liczby ustawiamy na pięciu miejscach na 5! sposobów.

W sytuacji II. dla sąsiadujących liczb parzystych wybieramy miejsca na 7 sposobów:

m₁ i m₂ , m₂ i m₃ , m₃ i m₄ , m₄ i m₅ , m₅ i m₆ , m₆ i m₇ , m₇ i m₈.

Miejsce dla trzeciej parzystej liczby możemy wybrać: na 5 sposobów wtedy, gdy parzyste liczby sąsiadują na miejscach m₁ i m₂ albo na miejscach m₇ i m₈ oraz na 4 sposoby w każdej z pozostałych możliwości.

Liczby parzyste możemy rozstawić na wybranych miejscach na 3! sposobów, a pozostałe liczby ustawiamy na pięciu miejscach na 5! sposobów.

Wszystkich zdarzeń elementarnych sprzyjających zdarzeniu A′ jest:

6 ⋅ 3! ⋅ 5! + 2 ⋅ 5 ⋅ 3! ⋅ 5! + 5 ⋅ 4 ⋅ 3! ⋅ 5!

Obliczamy prawdopodobieństwo zdarzenia A:

Zdający może wypisywać przypadki, w których wystąpią zdarzenia elementarne sprzyjające zdarzeniu A′, stosując metody analogiczne do metod III, IV, V z I sposobu rozwiązania, i uwzględnić 36 rozłącznych przypadków.

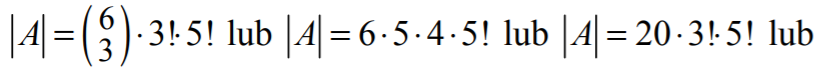
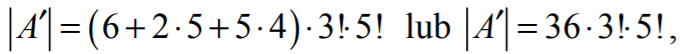
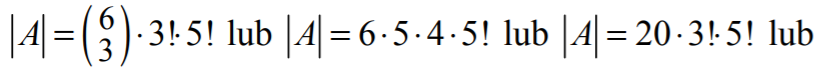
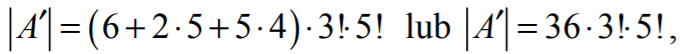
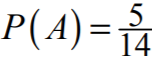
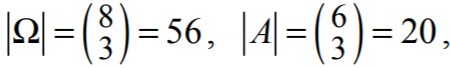
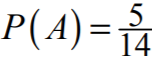
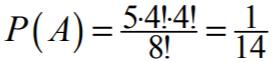
Zdający

• zapisze |Ω| = 8!

albo

• wypisze przynajmniej 11 różnych przypadków spośród 20, gdy rozpatruje zdarzenie A

albo

• wypisze przynajmniej 19 różnych przypadków spośród 36, gdy rozpatruje zdarzenie A′,

albo

• zapisze, że jest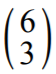lub 6⋅5⋅4 przypadków, gdy rozpatruje zdarzenie A

(lub 6 + 2⋅5 + 5⋅4 przypadków, gdy rozpatruje zdarzenie A′),

albo

• zapisze iloczyn 3!⋅5! lub w inny sposób zaznaczy uwzględnienie iloczynu 3!⋅5!, wynikającego z permutacji liczb parzystych i liczb nieparzystych na wybranych dla nich miejscach,

albo

• narysuje drzewo z wyróżnionymi co najmniej 11 różnymi istotnymi gałęziami odpowiadającymi zdarzeniu A (albo z wyróżnionymi co najmniej 19 różnymi istotnymi gałęziami odpowiadającymi zdarzeniu A'),

albo

• narysuje niepełne drzewo (może wystąpić brak istotnych gałęzi odpowiadających zdarzeniu A lub A'), ale na wszystkich odcinkach co najmniej jednej gałęzi zapisze prawdopodobieństwa, przy czym gałąź ta musi uwzględniać jeden z przypadków: wylosowano 3 parzyste liczby lub wylosowano 7 liczb i na tym zakończy lub dalej popełnia błędy.

Zdający

• zapisze |Ω| = 8! i wypisze przynajmniej 11 różnych przypadków spośród 20, gdy rozpatruje zdarzenie A,

albo

• zapisze |Ω| = 8! i wypisze przynajmniej 19 różnych przypadków spośród 36, gdy rozpatruje zdarzenie A′,

albo

• zapisze |Ω| = 8! i zapisze, że jest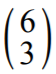lub 6⋅5⋅4 przypadków, gdy rozpatruje zdarzenie A (lub 6 + 2⋅5 + 5⋅4 przypadków, gdy rozpatruje zdarzenie A′),

albo

• zapisze

albo

• narysuje drzewo z wyróżnionymi co najmniej 11 różnymi istotnymi gałęziami odpowiadającymi zdarzeniu A (albo z wyróżnionymi co najmniej 19 różnymi istotnymi gałęziami odpowiadającymi zdarzeniu A') i na wszystkich odcinkach co najmniej jednej gałęzi zapisze prawdopodobieństwa, przy czym gałąź ta musi uwzględniać jeden z przypadków: wylosowano 3 parzyste liczby lub wylosowano 7 liczb i na tym zakończy lub dalej popełnia błędy.

Zdający

• zapisze |Ω| = 8! i zapisze

albo

• zapisze prawdopodobieństwo zdarzenia A (albo A') zgodnie z „metodą drzewkową”.

Zdający obliczy prawdopodobieństwo:

1. Możemy też rozpatrywać model probabilistyczny, w którym zdarzeniem elementarnym jest 3 elementowy podzbiór zbioru 8 elementowego (nie uwzględniamy wówczas kolejności ustawienia liczb nieparzystych ani kolejności ustawienia liczb parzystych, a jedynie pozycje zajmowane przez te liczby). Wtedy

2. Jeżeli zdający błędnie założy, że podany w treści zadania ośmioelementowy zbiór Z zawiera 4 liczby parzyste i 4 liczby nieparzyste (np. założy, że zbiór Z zawiera liczbę 8 zamiast 9) i rozwiąże zadanie do końca, otrzymując

to otrzymuje 2 punkty. Zdający otrzymuje w tej sytuacji 1 punkt tylko za zapisanie

|Ω| = 8!

3. Jeżeli zdający błędnie założy, że podany w treści zadania zbiór Z jest 9-elementowy (i zawiera 4 liczby parzyste i 5 liczby nieparzystych) i konsekwentnie rozwiąże zadanie do końca, to otrzymuje 3 punkty.

4. Jeżeli zdający zapisze |Ω|=8! oraz rozpatrując zdarzenie A′ rozważy trzy sytuacje:

I. wszystkie trzy liczby parzyste są kolejnymi wyrazami ciągu;

II. dwie liczby parzyste są dwoma skrajnymi (pierwszym i drugim lub siódmym i ósmym) wyrazami ciągu, a trzecia liczba parzysta nie sąsiaduje bezpośrednio z żadną z nich;

III. dwie liczby parzyste są dwoma kolejnymi, ale nie skrajnymi wyrazami ciągu, a trzecia parzysta nie sąsiaduje bezpośrednio z żadną z nich

oraz zapisze sposób zliczania tych ciągów w każdej z tych trzech sytuacji, uwzględniający permutacje liczb parzystych i liczb nieparzystych i jednoczenie gwarantujący to, że żaden ciąg nie zostanie policzony wielokrotnie; a ponadto nie ustali poprawnej liczby wszystkich zdarzeń elementarnych sprzyjających zdarzeniu A′, to otrzymuje 2 punkty.

5. Jeżeli zdający rozważa zdarzenie A i wypisuje przynajmniej 12 przypadków, ale jeden z nich zapisuje dwukrotnie, to otrzymuje przynajmniej 1 punkt. Dotyczy to także sytuacji wypisania 21 przypadków.