Odpowiedź:
Przykładowe rozwiązania
I sposób
Przyjmijmy oznaczenia jak na rysunku.
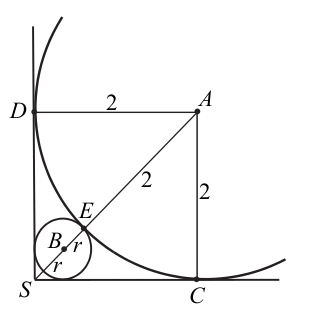
Wtedy |AS|=2√2 oraz |AE|=2. Zatem
|SE|=2√2–2.
Średnica okręgu o środku B i promieniu r jest krótsza od odcinka SE, więc
2r<2√2−2, czyli r<√2−1.
Co kończy dowód.
II sposób
Przyjmijmy oznaczenia jak na rysunku.

Wtedy |AS|=2√2 , BS=r√2 oraz AE=2.
Ponieważ |AS|=|BS|+|BE|+|AE| , więc otrzymujemy
2√2=r√2+r+2,
r(√2+1)=2√2−2.
Stąd mnożąc obie strony tego równania przez √2−1 otrzymujemy
r(√2+1)(√2−1)=2(√2−1)(√2−1)
r=2(√2−1)2,
r=2(2−2√2+1),
r=2(3−2√2).
Sprawdźmy, czy 2(3−2√2)<√2−1.
Przekształcamy tę nierówność równoważnie.
6−4√2<√2−1
7<5√2
schemat punktacji
Zdający otrzymuje 1 p.
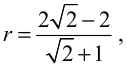
2. Jeżeli zdający błędnie przyjmie, że długość odcinka, którego jednym końcem jest punkt
styczności okręgów, a drugim wierzchołek kąta prostego, jest równa długości średnicy
mniejszego okręgu i nie wycofa się z tego założenia oraz nie obliczy długości wspomnianego
odcinka, to otrzymuje 0 punktów.
gdy:
• obliczy|SE|=2√2–2.
albo
• zapisze równość 2√2=r√2+r+2
i na tym zakończy lub dalej popełni błędy.
Zdający otrzymuje 2 p.
gdy przeprowadzi pełny dowód.
gdy przeprowadzi pełny dowód.
Uwagi:
1. Jeżeli zdający poprawnie obliczy r i zapisze wynik w postaci ułamka, w którym w mianowniku występuje liczba niewymierna, np.
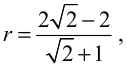
i błędnie szacuje tę liczbę, np. stosując takie same przybliżenia z niedomiarem √2 w liczniku i w mianowniku, to otrzymuje 1 punkt.